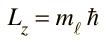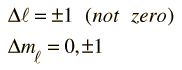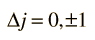Reglas de Selección en las Transiciones Electrónicas
En los fenómenos espectrales tales como el efecto Zeeman, se hace evidente que las transiciones no se observan entre todos los pares de niveles de energía. Algunas transiciones están "prohibidas", (es decir, altamente improbable), mientras que otras están "permitidas" por un conjunto de reglas de selección. El número de componentes separadas observadas en el efecto Zeeman, es consistente con las reglas de selección:
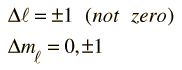
Estas son las reglas de selección para una transición dipolar eléctrica. Se puede decir que el campo eléctrico oscilante asociado con las transiciones, se asemeja a un dipolo eléctrico oscilante. Cuando esto se expresa en términos cuánticos, la emisión de fotones está siempre acompañada por un cambio de 1 en el número cuántico del momento angular orbital. El número cuántico magnético puede cambiar por cero o una unidad.
Otro enfoque en las reglas de selección es, tener en cuenta que cualquier transición de electrones que implique la emisión de un fotón, debe implicar un cambio de 1 en el momento angular. Se dice que el fotón tiene un momento angular intrínseco, o "spin", de uno, por lo que la conservación del momento angular en la emisión de fotón, requiere un cambio de 1 en el momento angular del átomo. El número cuántico del espín del electrón no cambia en estas transiciones, por lo que una regla de selección adicional es:

El momento total angular puede cambiar por cero o uno:
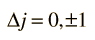 Una excepción a esta última regla de selección es, que no se puede tener una transición desde j=0 a j=0; es decir, como el vector del momento angular debe cambiar en una unidad en una transición electrónica, j=0 -> 0 no puede suceder, porque no hay momento angular total para re-orientar y conseguir un cambio de 1.
Una excepción a esta última regla de selección es, que no se puede tener una transición desde j=0 a j=0; es decir, como el vector del momento angular debe cambiar en una unidad en una transición electrónica, j=0 -> 0 no puede suceder, porque no hay momento angular total para re-orientar y conseguir un cambio de 1.
|
Índice
Conceptos de la Ecuación de Schrödinger
Conceptos del Hidrógeno
Conceptos de Estructura Atómica |