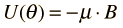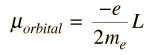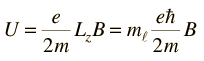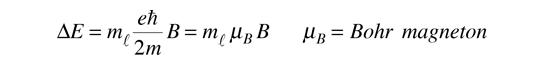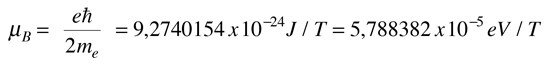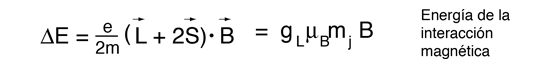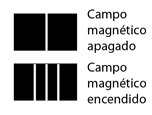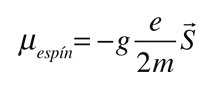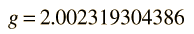Interacción Zeeman
Un campo magnético externo ejerce un par sobre un dipolo magnético, y la energía potencial magnética resultante es
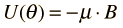
El momento de dipolo magnético asociado con el momento angular orbital, está dado por
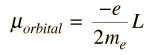
Para el campo magnético en la dirección z esto da
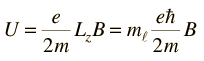
Teniendo en cuenta la cuantización del momento angular, esto da unos niveles de energía equidistantes, desplazados desde el nivel de campo cero por
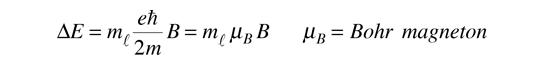
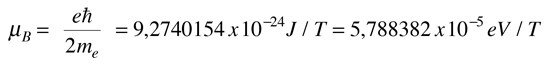
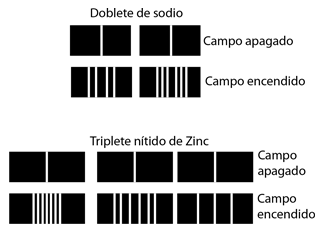
Este desplazamiento de los niveles de energía, da el desdoblamiento multiplete uniformemente espaciado de las líneas espectrales, que se llama efecto Zeeman.
El campo magnético también interactúa con el momento magnético del espín electrónico, por lo que en muchos casos también contribuye al efecto Zeeman. El espín del electrón no se había descubierto en el momento de los experimentos originales de Zeeman, por lo que los casos en los que contribuían, eran considerados anómalos. El término "efecto Zeeman anómalo" se ha mantenido para los casos en que contribuyen al espín. En general, están involucrados tanto los momentos orbital como de espín, y la interacción Zeeman toma la forma
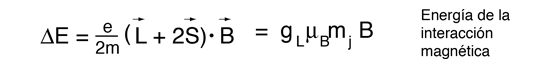
El factor de dos multiplicando al momento angular del espín electrónico, viene del hecho de que es dos veces más eficaz en la producción del momento magnético. Este factor es llamado factor g del espín, o ratio giromagnético. Aquí la evaluación del producto escalar entre el momento angular y el campo magnético se complica, por el hecho de que los vectores S y L están ambos precediendo alrededor del campo magnético, y no están en general en la misma dirección. Los persistentes primeros espectroscopistas, elaboraron una manera de calcular el efecto de las direcciones. El factor geométrico resultante gL en la expresión final de arriba, se denomina factor de Landé g. Les permitió expresar los desdoblamientos resultantes de las líneas espectrales, en términos de la componente z del momento angular total, mj.
El tratamiento de arriba del efecto Zeeman, describe el fenómeno cuando los campos magnéticos son lo suficientemente pequeños, para que los momentos angular orbital y de espín, se puedan considerar acoplados. Para los campos magnéticos extremadamente fuertes, este acoplamiento se rompe, y debe ser tomado otro enfoque. El efecto de campo fuerte, se llama efecto Paschen-Back.
|
Índice
Conceptos de la Ecuación de Schrödinger |