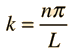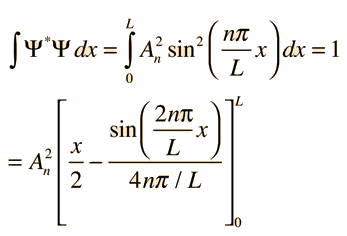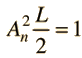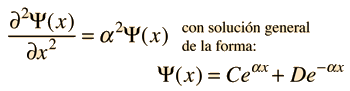Partícula en una Caja
 |
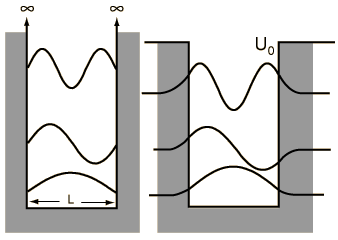
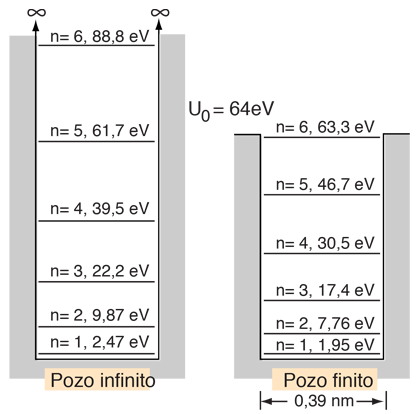
Supóngase que el potencial U(x) en la ecuación de Schrödinger independiente del tiempo es cero, en el interior de una caja unidimensional de longitud L, e infinito fuera de la caja. Para una partícula en el interior de la caja, es apropiada una función de onda partícula libre, pero como la probabilidad de encontrar la partícula fuera de la caja es cero, la función de onda debe ir a cero en las paredes. Esto limita la forma de la solución a 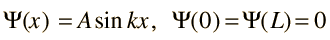
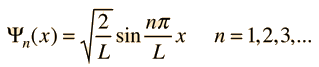 |
| Estudio del Significado | Energías Cuantizadas | Energías de Contención | Caja de Paredes Finitas |
| Partícula en una Caja 3-D |
Conceptos de la Ecuación de Schrödinger
| HyperPhysics*****Física Cuántica | M Olmo R Nave |