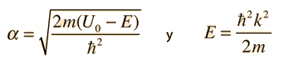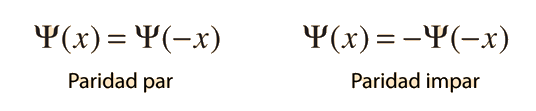Partícula en una Caja de Pared Finita

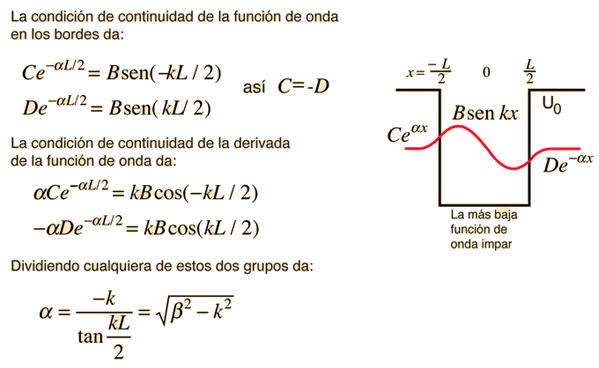
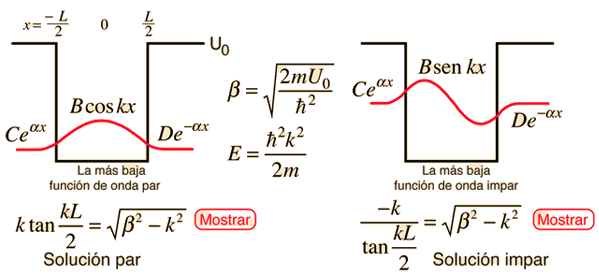
Dado un pozo de potencial como el que se muestra, y una partícula con energía menor que la altura del pozo, las soluciones con respecto al centro del pozo, pueden ser de cualquiera clase de paridad, par, o impar. La ecuación de Schrödinger da formas trancendentales para ambos casos, por lo que se deben utilizar métodos de solución numérica.

Solución Par, Caja Finita

Este último paso, hace uso de la sustitución que se utilizó en la configuración del problema del pozo finito:

Las limitaciones sobre la función de onda común, requieren que tanto la función de onda, como su derivada, sean continuas en cualquier punto. La aplicación de estas restricciones, es a menudo la manera en que la solución se ve obligada a adaptarse a la situación física.

Solución Numérica del Estado Fundamental

La solución del estado fundamental de un pozo de potencial finito, es el estado más bajo de paridad par y se puede expresar en la forma donde Dado que ambos lados de la ecuación son dependientes de la energía E, para la cual se está buscando la solución, la ecuación es trancendental y debe resolverse numéricamente. Una forma de estimar la energía del estado fundamental de un pozo de potencial finito, es usar la energía de pozo infinito, para producir un factor de atenuación de ensayo α. Luego, el valor de α puede ser refinado por iteración, para obtener una anchura de pozo efectivo, y una solución numérica de la energía.

Solución Impar, Caja Finita

Este último paso hace uso de la sustitución que se usó en la configuración del problema del pozo finito:

Las limitaciones sobre la función de onda común, requieren que tanto la función de onda, como su derivada, sean continuas en cualquier punto. La aplicación de estas restricciones, es a menudo la manera en que la solución se ve obligada a adaptarse a la situación física.

Paridad y Partícula en una Caja

En el caso unidimensional, la paridad se refiere a la "homogeneidad" o "rareza" de una función con respecto a la reflexión alrededor de x = 0.

El problema de la partícula en una caja, puede dar una idea de la importancia de la paridad en la mecánica cuántica. La caja tiene una línea de simetría, hacia abajo del centro de la misma (x = 0). Las consideraciones básicas de la simetría, demandan que la probabilidad de encontrar la partícula en -x, sea la misma que en x. La condición sobre la probabilidad está dada por:

Esta condición se satisface si la paridad es par o impar, pero no, si la función de onda es una combinación lineal de funciones pares e impares. Esto se puede generalizar afirmando que en el problema físico, las funciones de onda deben tener una paridad definida con respecto a las operaciones de simetría.