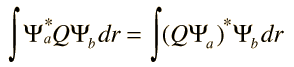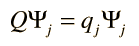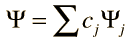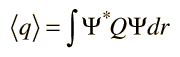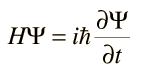Postulado del Operador

Con cada observable físico, hay asociado un operador matemático que se utiliza en conjunción con la función de onda. Supóngase que la función de onda asociada con un valor cuantizado definido (valor propio) del observable se denota por Ψ_n, y el operador se representa por Q. La acción del operador está dado por

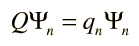
El operador matemático Q, extrae el valor observable q_n, mediante la operación sobre la función de onda que representa ese estado particular del sistema. Este proceso tiene consecuencias sobre la naturaleza de la medición en un sistema mecánico cuántico. Cualquier función de onda para el sistema, se puede representar como una combinación lineal de las funciones propias Ψ_n (véase postulado de conjunto básico), por lo que el operador Q se puede utilizar para extraer una combinación lineal de valores propios, multiplicado por los coeficientes relacionados con la probabilidad de que sean observados (véase postulado de valor esperado).

Postulado de Propiedad Hermítica

El operador mecánico cuántico Q asociado con una propiedad medible, debe ser hermítico (hermitiano). Matemáticamente esta propiedad está definida por

donde Ψ_a y Ψ_b son funciones normalizables arbitrarias, y la integración se extiende a todo el espacio. Físicamente, la propiedad hermitiana es necesaria para que los valores medidos (valores propios) se vean limitados a números reales.

Postulado de Conjunto Básico

El conjunto de funciones Ψ_j que son funciones propias de la ecuación de valor propio

forman un conjunto completo de funciones linealmente independientes. Se puede decir que forman un conjunto básico, en términos del cual, se puede expresar cualquier función de onda que represente al sistema:

Esto implica que cualquier función de onda Ψ representando un sistema físico, se puede expresar como una combinación lineal de las funciones propias de cualquier observable físico del sistema.

Postulado de Valor Esperado

En un sistema físico descrito por una función de onda Ψ , el valor esperado de cualquier observable físico q, puede ser expresado en términos del correspondiente operador Q como sigue:

Se supone aquí que la función de onda está normalizada, y que la integración se extiende a todo el espacio. Este postulado sigue a lo largo de las líneas del postulado del operador y el postulado de conjunto básico. La función se puede representar como una combinación lineal de funciones propias de Q, y los resultados de la operación proporciona los valores físicos multiplicado por el coeficiente de probabilidad. Dado que la función de onda está normalizada, la integral proporciona una media ponderada de los valores observables posibles.

Postulado de Evolución Temporal

Si Ψ es la función de onda de un sistema físico en un momento inicial, y el sistema está libre de interacciones externas, entonces, la evolución con el tiempo de la función de onda viene dada por

donde H es el operador hamiltoniano formado del hamiltoniano clásico, mediante la sustitución de los correspondientes operadores mecánico-cuánticos, por sus observables clásicos. Para un sistema mecánico, el hamiltoniano clásico sería solo la energía cinética más la energía potencial, es decir, la expresión de energía. El papel del hamiltoniano en ambos espacio y tiempo, está contenido en la ecuación de Schrodinger.