Valores Esperados
Para relacionar el cálculo de la mecánica cuántica a algo que se pueda observar en el laboratorio, se calcula el "valor esperado" de los parámetros medibles. Para la posición x, el valor esperado se define como
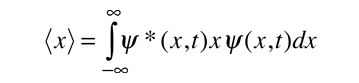
Esta integral puede interpretarse como el valor medio de x, que se esperaría obtener a partir de un gran número de mediciones. Alternativamente, podría verse como el valor medio de posición para un gran número de partículas, que están descritas mediante la misma función de onda. Por ejemplo, el valor esperado del radio del electrón en el estado fundamental del átomo de hidrógeno, es el valor medio que se espera obtener al realizar la medición sobre un gran número de átomos de hidrógeno.
Mientras que el valor esperado de una función de posición, tiene la apariencia de un promedio de la función, el valor esperado del momento implica la representación del momento como un operador de la mecánica cuántica.
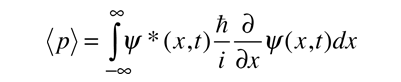
donde
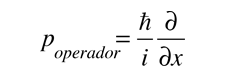
es el operador de la componente x del momento.
Como la energía de una partícula libre está dada por

el valor esperado de la energía viene a ser
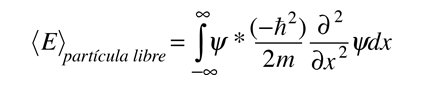
para una partícula en una dimensión.
En general, el valor esperado de cualquier cantidad observable, se halla poniendo el operador mecánico-cuántico de ese observable, en la integral de la función de onda sobre el espacio:
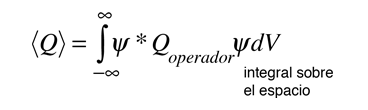
Conceptos de la Ecuación de Schrödinger
Postulados de la Mecánica Cuántica
| HyperPhysics*****Física Cuántica | M Olmo R Nave |