Oscilador Armónico Cuántico: Mínima Energía por el Principio de Incertidumbre

La energía del estado fundamental del oscilador armónico cuántico, se puede demostrar que corresponde con la mínima energía permitida por el principio de incertidumbre.

La energía del oscilador armónico cuántico debe ser al menos

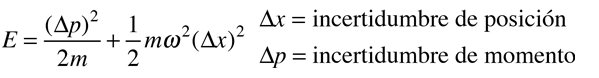
Tomando el límite inferior del principio de incertidumbre

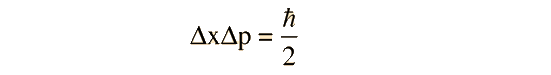
Luego, la energía expresada en términos de la incertidumbre de la posición, se puede escribir

Para minimizar esta energía, se toma la derivada de la energía respecto de la posición y se iguala a cero, dando

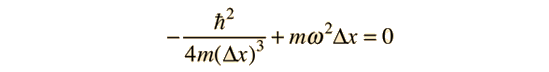
Resolviendo para la incertidumbre de la posición, da

Sustituyendo, da el valor mínimo de la energía permitida.

Este es un resultado físico muy importante, ya que nos dice que la energía de un sistema descrito por un potencial de oscilador armónico, no puede tener un valor cero. Los sistemas físicos tales como los átomos en una red sólida o las moléculas poliatómicas en un gas, no puede tener energía cero incluso a la temperatura del cero absoluto. La energía del estado vibracional fundamental, es referida a menudo como "vibración de punto cero". La energía de punto cero, es suficiente para evitar que el helio-4 líquido, se congele a la presión atmosférica, no importa cuán baja sea la temperatura.