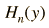Oscilador Armónico Cuántico: Ecuación de Schrodinger

Se puede obtener la ecuación de Schrodinger de un oscilador armónico, utilizando el potencial en un muelle clásico

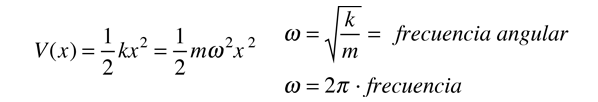
La ecuación de Schrodinger con esta forma de potencial es

Dado que la derivada de la función de onda, debe devolver el cuadrado de x más una constante multiplicada por la función original, se sugiere la siguiente forma:

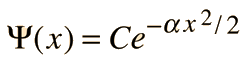
Téngase en cuenta que esta forma (una función gaussiana), satisface el requisito de ir a cero en el infinito, por lo que es posible normalizar la función de onda.

Sustituyendo esta función en la ecuación de Schrodinger y estableciendo las condiciones de contorno, resulta la energía del estado fundamental del oscilador armónico cuántico:

Mostrar

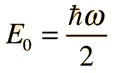Aunque este proceso muestra que esta energía satisface la ecuación Shrodinger, no demuestra que es la energía más baja. Una forma interesante de verlo, es demostrar que es la energía más baja permitida por el principio de incertidumbre.

La solución general de la ecuación de Schrödinger, conduce a una secuencia de niveles de energía uniformemente espaciados, que se caracterizan por el número cuántico n.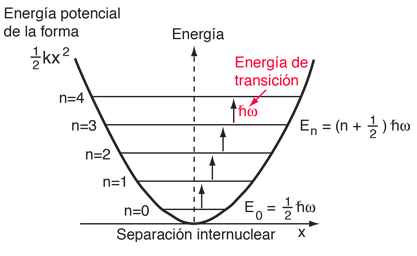

Las funciones de onda del oscilador armónico cuántico, contienen la forma gaussiana que les permite satisfacer las condiciones de contorno necesarias en el infinito. En la función de onda asociada con un valor dado del número cuántico n, el gaussiano es multiplicado por un polinomio de orden n, llamado polinomio de Hermite. Las expresiones se simplifican mediante la sustitución

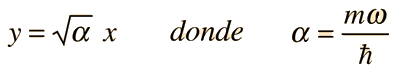
La fórmula general de las funciones de onda normalizadas es

= Polinomio de Hermite

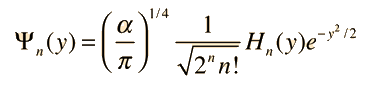El oscilador armónico cuántico tiene implicaciones más allá de la simple molécula diatómica. Es la base para la comprensión de los modos complejos de vibración en las moléculas más grandes, el movimiento de los átomos en una red sólida, la teoría de la capacidad calorífica, etc. En los sistemas reales, los espaciamientos de energía son solamente iguales en los niveles mas bajos, donde el potencial es una buena aproximación al potencial armónico del tipo de "masa sobre un muelle". Los términos inarmónicos que aparecen en el potencial de una molécula diatómica, son útiles para mapear el potencial detallado de tales sistemas.