Oscilador Armónico Cuántico: Solución del Estado Fundamental

Para encontrar la solución al estado fundamental de la ecuación de Schrodinger del oscilador armónico cuántico

se prueba con la siguiente fórmula para la función de onda

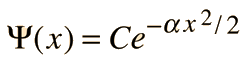
sustituyendo esta función en la ecuación de Schrodinger, mediante la evaluación de la derivada segunda,

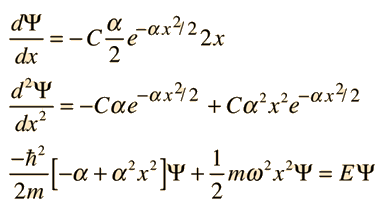
Para que esto sea una solución a la ecuación de Schrödinger para todos los valores de x, los coeficientes de cada potencia de x deben ser iguales. Eso nos da un método para fijar las condiciones de contorno de la ecuación diferencial. Estableciendo los coeficientes del cuadrado de x iguales entre sí:

Luego, estableciendo los términos constantes iguales, da la energía

Esta es la energía mas pequeña permitida por el principio de incertidumbre. Mostrar

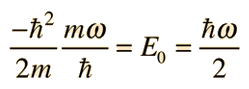Este es un resultado físico muy importante, ya que nos dice que la energía de un sistema descrito por un potencial de oscilador armónico, no puede tener un valor cero. Los sistemas físicos tales como los átomos en una red sólida o las moléculas poliatómicas en un gas, no puede tener energía cero incluso a la temperatura del cero absoluto. La energía del estado vibracional fundamental, es referida a menudo como "vibración de punto cero". La energía de punto cero, es suficiente para evitar que el helio-4 líquido, se congele a la presión atmosférica, no importa cuán baja sea la temperatura.