Series de Taylor

Si f(x) es una función de buen comportamiento* alrededor de un elegido punto de expansión x₀, entonces la función se puede expandir en una serie llamada serie de Taylor:

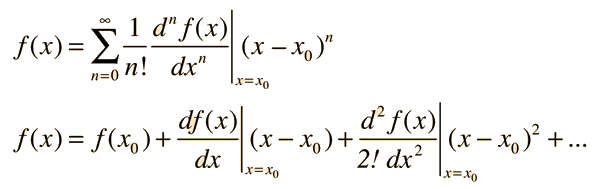
La serie de Taylor de una función es a menudo útil en situaciones físicas donde se desee obtener el valor aproximado de la función alrededor del punto de expansión x₀. Se puede evaluar término a término en términos de las derivadas de la función. Es típico que los términos sucesivos en una aproximación en serie de una función sean cada vez mas y mas pequeños, y cuando el valor del siguiente término se considere despreciable en términos del problema que se aborda, entonces uno puede juzgar que se ha logrado una aproximación suficientemente exacta de la función.

Es frecuente el caso donde un conveniente punto de expansión es x₀ = 0, y la serie alrededor de este punto de expansión especial se le llama también serie de Maclaurin. Hay muchas aplicaciones para expansiones de funciones comunes alrededor de x=0. Algunos ejemplos son:

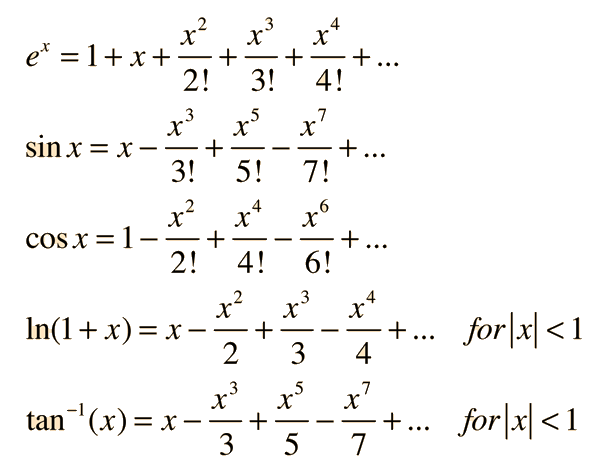
La aproximación de un término en las series de funciones trigonométricas tiene muchas aplicaciones como las "aproximaciones de ángulos pequeños".

* Buen comportamiento significa que tanto la función como sus derivadas son continuas y están definidas en el intervalo de expansión alrededor de x₀.