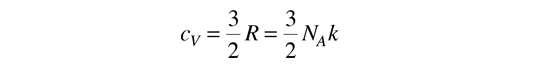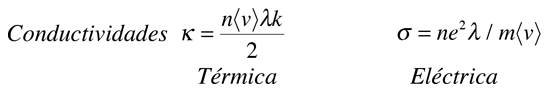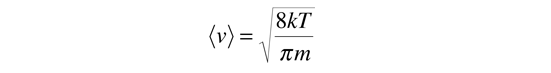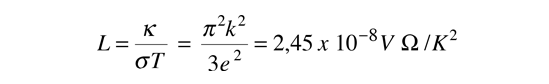Conductividad Térmica
La transferencia de calor por conducción, consiste en la transferencia de energía dentro de un material, sin ningún tipo de movimiento del material en su conjunto. La tasa de transferencia de calor depende del gradiente de temperatura y la conductividad térmica del material. La conductividad térmica es un concepto bastante sencillo cuando se está estudiando la pérdida de calor a través de las paredes de una casa, y se pueden encontrar tablas que caracterizan a los materiales de construcción, y que nos permiten hacer cálculos razonables
Las preguntas más fundamentales surgen, cuando se examinan las razones sobre las amplias variaciones en la conductividad térmica. Los gases transfieren el calor por las colisiones directas entre las moléculas, y como era de esperar, su conductividad térmica es baja en comparación con la mayoría de los sólidos, ya que estos constituyen un medio diluido. Los sólidos no metálicos transfieren el calor por vibraciones reticulares, de modo que no hay movimiento neto del medio cuando la energía se propaga a su través. Esa transferencia de calor a menudo se describe en términos de "fonones" -los cuantos de vibraciones de la red-. Los metales son mucho mejores conductores térmicos que los no metales, porque los mismos electrones móviles que participan en la conducción eléctrica, también participan en la transferencia de calor.
Conceptualmente, la conductividad térmica se puede establecer como una propiedad dependiente del medio, que relaciona la velocidad de pérdida de calor por unidad de área, con la velocidad de cambio de la temperatura.
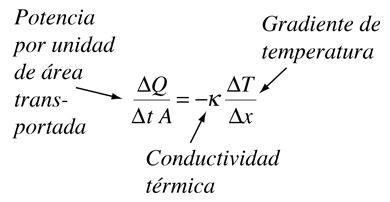 |
|
En un gas ideal, la velocidad de transferencia de calor es proporcional a la velocidad molecular media, el camino libre medio y la capacidad calorífica molar del gas.
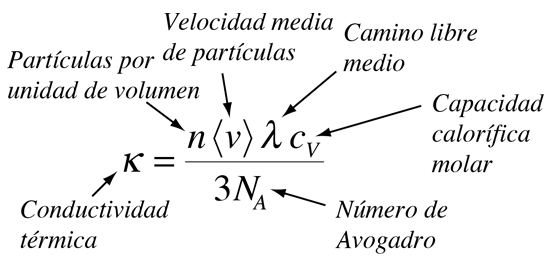
En los sólidos no metálicos, la transferencia de calor se estima que se realiza a través de las vibraciones de la red cristalina del sólido. En esta transferencia, los átomos de una parte del sólido que están vibrando mas energicamente, transfiere esa energía hacia los atomos vecinos menos energéticos. Esto se puede mejorar por el movimiento cooperativo en forma de propagación de ondas de la red atómica, que son cuantizadas como fonones. En la práctica hay tanta variedad en los sólidos no metálicos que cuando hacemos cálculos ordinarios, caracterizamos a las sustancias por la medida de la conductividad térmica.
La conductividad térmica de los metales, es bastante alta y aquellos metales que son los mejores conductores eléctricos son tambien, los mejores conductores térmicos. A una determinada temperatura, las conductividades térmicas y eléctricas de los metales son proporcionales, pero aumentando la temperatura, aumenta la conductividad térmica mientras disminuye la conductividad eléctrica. Este comportamiento está cuantificado en la ley de Wiedemann-Franz:
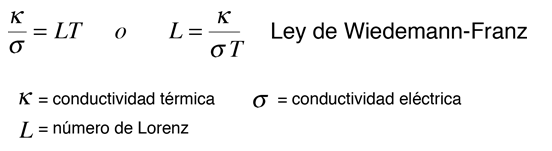
donde la constante de proporcionalidad L, se llama número de Lorenz. Cualitativamente, esta relación está basada en el hecho de que tanto en el transporte calorífico como el eléctrico, están implicados los electrones libres del metal. La conductividad térmica aumenta con la velocidad media de las partículas porque estas aumenta el transporte de energía. Sin embargo, la conductividad eléctrica disminuye con el aumento de velocidad de las partículas, porque las colisiones desvian los electrones del camino de transporte de cargas. La proporción de la conductividad térmica a la eléctrica, depende del cuadrado de la velocidad media, la cual es proporcional a la temperatura cinética.
| Tabla de Conductividad Térmica |
Conceptos sobre Transferencia del Calor
Ejemplos sobre Transferencia del Calor
| HyperPhysics*****Termodinámica | M Olmo R Nave |