Identidades del Cálculo Vectorial
La divergencia del rotacional es igual a cero:

El rotacional del gradiente es igual a cero:
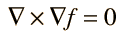
| Mas Identidades Vectoriales |
Cálculo Vectorial
| HyperPhysics*****HyperMath*****Cálculo | M Olmo R Nave |
Identidades del Cálculo VectorialLa divergencia del rotacional es igual a cero:  El rotacional del gradiente es igual a cero: 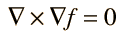
|
Índice Cálculo Vectorial | ||
|
Atrás |
Teorema de la DivergenciaLa integral de volumen de la divergencia de una función vectorial es igual a la integral sobre la superficie de la componente normal a la superficie.
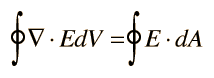 |
Índice Cálculo Vectorial | ||
|
Atrás |
Teorema de Stokes La integral de área del rotacional de una función vectorial es igual a la integral de línea del campo alrededor del perímetro del área.
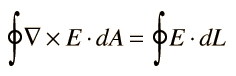 |
Índice Cálculo Vectorial | ||
|
Atrás |
Identidades VectorialesEn las siguientes identidades u y v son funciones escalares, mientra que A y B son funciones vectoriales. La sobrebarra muestra el alcance de la operación del operador nabla.  |
Índice Cálculo Vectorial | ||
|
Atrás |