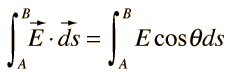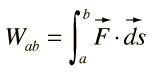Integral de Área
 |
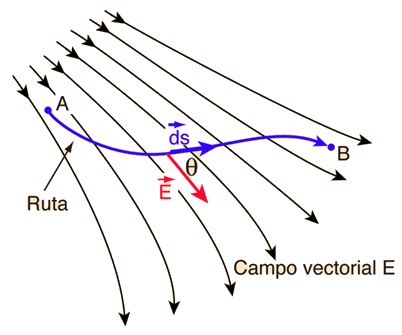
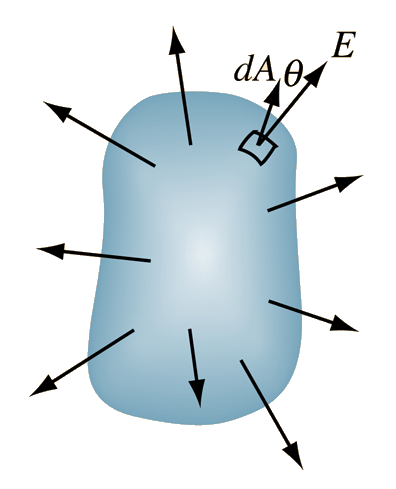
La integral de área de una función vectorial E, se define como la integral sobre una superficie del producto escalar de E, por el elemento de área dA. La dirección del elemento de área es perpendicular al área en ese punto de la superficie. |
La integral de superficie dirigida hacia fuera sobre una superficie cerrada completa se denota por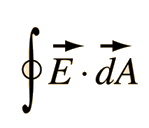 |
 |
| HyperPhysics*****HyperMath*****Cálculo | M Olmo R Nave |