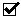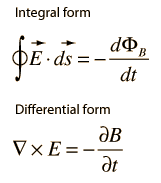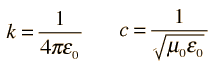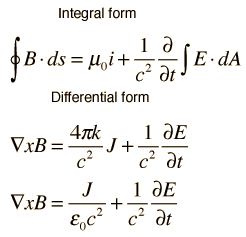Ley de Gauss para la Electricidad
|
El flujo eléctrico exterior de cualquier de cualquier superficie cerrada es proporcional a la carga total encerrada dentro de la superficie. La fórmula integral de la ley de Gauss encuentra aplicación en el cálculo de los campos eléctricos alrededor de los objetos cargados. Cuando se aplica la ley de Gauss a un campo eléctrico de una carga puntual, se puede ver que es consistente con la ley de Coulomb. Mientras que la integral de área del campo eléctrico da una medida de la carga neta encerrada, la divergencia del campo eléctrico da una medida de la densidad de las fuentes. También tiene implicaciones en la conservación de la carga. |
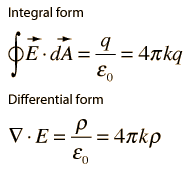
|
| Ecuaciones de Maxwell |
Conceptos sobre las Ecuaciones de Maxwell
| HyperPhysics*****Electricidad y Magnetismo | M Olmo R Nave |