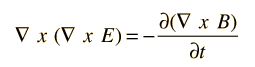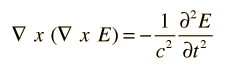Conservación de la Carga

En las ecuaciones de Maxwell está contenidad la idea fundamental de la conservación de la carga. Si tomamos la divergencia de la forma diferencial de la ley de Ampere:

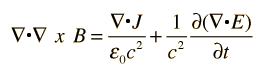
El primer término de arriba es cero por identidad, y usando la ley de Gauss:

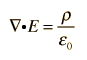
el resultado es:

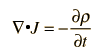
De aquí se implica que la corriente a través de cualquier superficie cerrada es igual a la velocidad de cambio de la carga en el interior de la superficie. Esto es una prueba importante de las ecuaciones de Maxwell, puesto que toda la evidencia experimental apunta hacia la conservación de la carga.

La Ecuación de Onda

Las ecuaciones de Maxwell contienen la ecuación de onda de las ondas electromagnéticas. Una forma de obtener esta ecuación de onda:

1. Tomamos el rotacional de la ley de Faraday:

2. Sustituimos por la ley de Ampere para una región de carga sin corriente:

Esto es una ecuación de onda tridimensional en forma vectorial. Es difícil visualizarlo de esta forma. Resulta mas familiar cuando se reduce a una onda plana con el campo en la dirección x solamente:

Puesto que el campo eléctrico está solamente en la dirección x, la propagación es perpendicular al eje x y puede tomar cualquier dirección en el plano yz, dependiendo de los valores de las derivadas. Esta ecuación es la forma general de la ecuación de onda bidimensional.