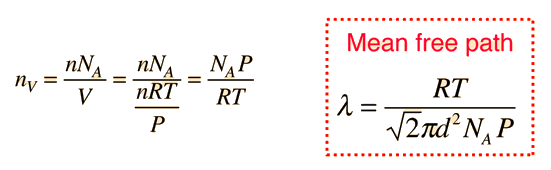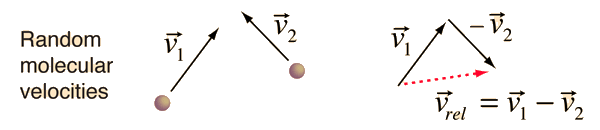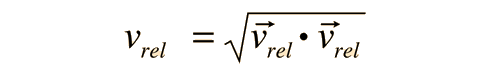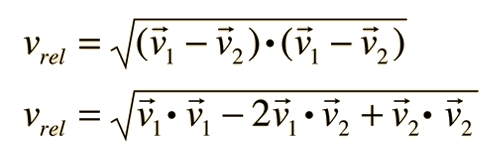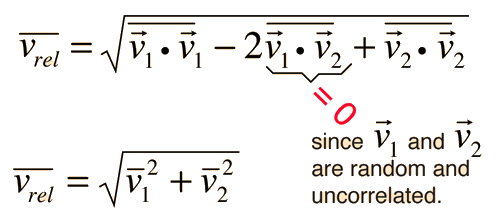Mean Free Path

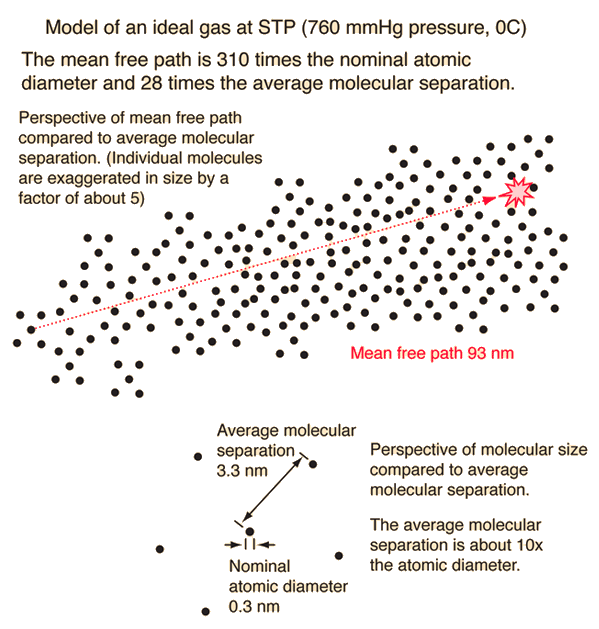
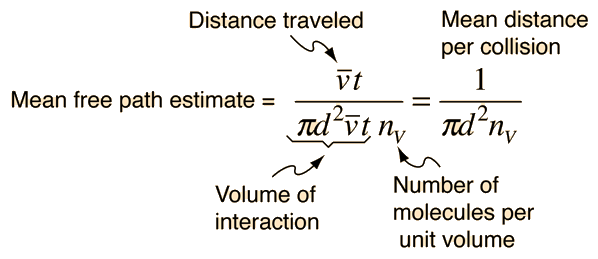
The mean free path or average distance between collisions for a gas molecule may be estimated from kinetic theory. Serway's approach is a good visualization - if the molecules have diameter d, then the effective cross-section for collision can be modeled by

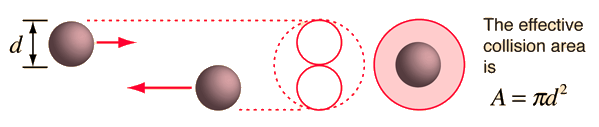
using a circle of diameter 2d to represent a molecule's effective collision area while treating the "target" molecules as point masses. In time t, the circle would sweep out the volume shown and the number of collisions can be estimated from the number of gas molecules that were in that volume.

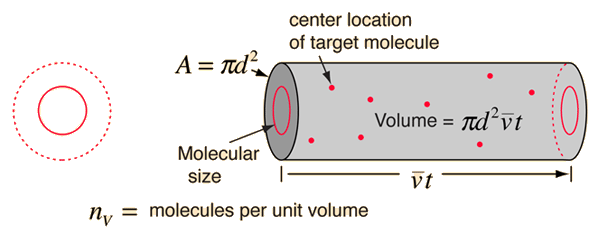
The mean free path could then be taken as the length of the path divided by the number of collisions.

The problem with this expression is that the average molecular velocity is used, but the target molecules are also moving. The frequency of collisions depends upon the average relative velocity of the randomly moving molecules.

Refinement of Mean Free Path

The intuitive development of the mean free path expression suffers from a significant flaw - it assumes that the "target" molecules are at rest when in fact they have a high average velocity. What is needed is the average relative velocity, and the calculation of that velocity from the molecular speed distribution yields the result

Show

which revises the expression for the effective volume swept out in time t

The number of molecules per unit volume can be determined from Avogadro's number and the ideal gas law, leading to

It should be noted that this expression for the mean free path of molecules treats them as hard spheres, whereas real molecules are not. For noble gases, the collisions are probably close to being perfectly elastic, so the hard sphere approximation is probably a good one. But real molecules may have a dipole moment and have significant electrical interaction as they approach each other. This has been approached by using an electrical potential for the molecules to refine the calculation, and also by using the measured viscosity of the gas as a parameter to refine the estimate of the mean free path of molecules in real gases.

Reference:

Wiki: mean free path

Wiki: viscosity

Gas viscosity

Mean Free Path Calculation

Mean Free Path Perspective

You may be surprised by the length of the mean free path compared to the average molecular separation in an ideal gas. An atomic size of 0.3 nm was assumed to calculate the other distances.

Average Relative Velocity

In order to calculate the mean free path for a molecule of a gas, it is necessary to assess the average relative velocity of the molecules involved rather than just the average velocity of any given molecule. The relative velocity of any two molecules can be expressed in terms of their vector velocities.

The magnitude of the relative velocity can be expressed as the square root of the scalar product of the velocity with itself.

This expression can be expanded as follows.

Taking the average of the terms leads to

Since the same average velocity would be associated with each molecule, this becomes