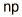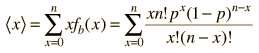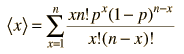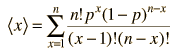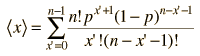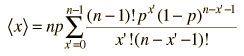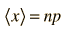The Mean
The value you expect to get in a statistical experiment is the mean. If you toss a coin 10 times, you expect to get 5 heads and 5 tails. The mean is often called the "expected value" or the "expectation value". You expect this value because the probability of getting "heads" is 0.5 and if you toss 10 times you should get 5. To formalize this particular example of the mean, if p is the probability and n the number of events, then the mean is a = np. This is the form of the mean when the probability can be expressed by the binomial distribution.
To formalize the concept a bit more, if for an experiment with discrete outcomes xi for which the probability is P(xi), then the mean is given by
a = ΣxiP(xi)
For the case of continuous variables where the probability is expressed in terms of a distribution function, the mean takes the form

Applied statistics concepts
| HyperPhysics*****HyperMath*****Algebra | R Nave |