Orbit Speed Inside and Outside a Mass Distribution
The orbit speed of an object is a measure of the amount and distribution of the mass that is attracting it gravitationally. To examine this dependence, consider a sphere of uniform density ρ which is diffuse enough to permit the orbiting of a mass m within the radius of the mass distribution. For this idealized case, the inverse square law form of the law of gravity along with the centripetal force relationship can be used to calculate the orbit velocity for a circular orbit. This calculation is made possible by the fact that the orbiting mass experiences a net attraction only by that mass inside its orbit, and the mass outside its orbit exerts a net zero force.
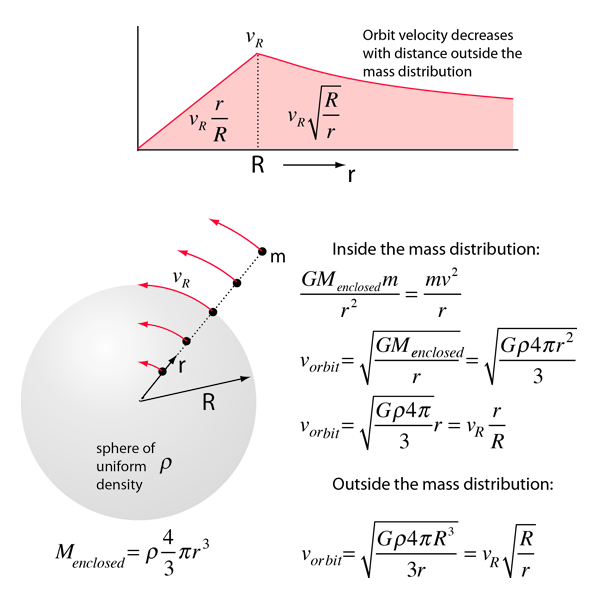
Upon calculating the circular orbit velocity, we find that inside the spherical mass distribution, the orbit velocity increases with radius, reaching a maximum at the radius of the mass distribution. Then if falls off as the radius increases, following the relationship:
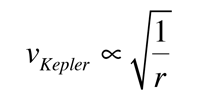
This calculation was done for a spherical mass, but for a uniform disc of mass like an idealized galaxy, the orbital velocity of material outside the detectable mass of the galaxy would be expected to fall off as some factor times the inverse square root of the radius. Surprisingly, the orbital velocity does not fall off at the edge of the detectable matter, staying almost constant well beyond the detectable edge of the galaxy. This is the nature of the evidence for dark matter which exceeds the visible matter by about a factor of six.
| Force on a mass outside a spherical shell |
| Example of falling through the Earthl |
Newton's laws
Gravity concepts
| HyperPhysics***** Mechanics | R Nave |