Angular Momentum Demonstrations
The subject of mechanics depends strongly upon the conservation laws, such as conservation of energy, conservation of momentum, and conservation of angular momentum. The first two demonstrations show the conservation of angular momentum, and the third shows the vector nature of angular momentum when an unbalanced torque acts on the system.
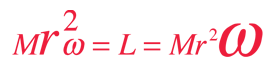 As an example of the mechanics of angular momentum, spinning on a stool with masses held out demonstrates conservation of angular momentum. Bringing the masses in makes the stool spin faster. The angular momentum is equal to the moment of inertia times the angular velocity, so if you reduce the moment of inertia by a factor of two by pulling the masses in, the spin speed will double. |  |
 | Another way to demonstrate conservation of angular momentum is to spin a wheel and hold it on the rotatable stool. If you turn the wheel over to reverse the direction of its angular momentum, then the stool counter-rotates to keep the vector angular momentum the same. In the ideal case of no frictional torque from the stool, the total angular momentum of the system must remain the same in both magnitude and direction. |
If a spinning wheel is supported on an axis point so that there is a net torque on it, the torque will change the angular momentum in a manner which is called "precession". Both angular momentum and torque are vector quantities, and if the applied torque has a component perpendicular to the angular momentum, it will produce a rate of change of the direction of the spin axis. | 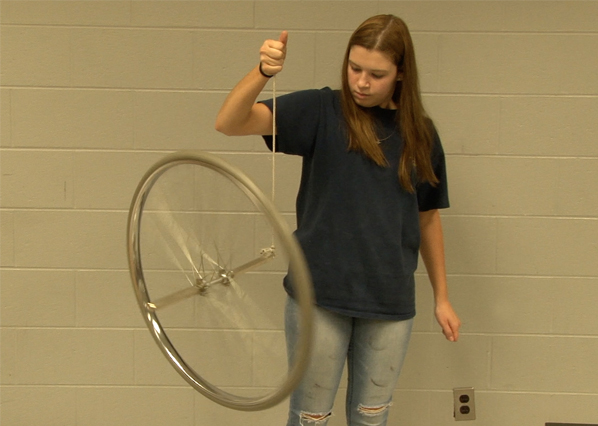 |
Conservation of angular momentum
| HyperPhysics***** Mechanics | J Nave, R Nave |