Freefall Velocity with Quadratic Drag
A freely falling object will be presumed to experience an air resistance force proportional to the square of its speed. The downward direction will be taken as positive, and the velocity as a function of time is the object of the calculation. The expressions will be developed for the two forms of air drag which will be used for trajectories:
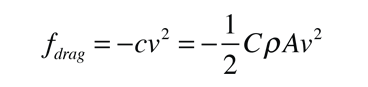
although the first steps will be done with just the form -cv2 for simplicity.
The differential equation for the motion is

which expresses the force in terms of the terminal velocity vt:
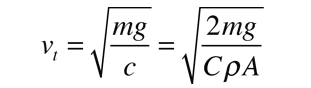
Integrating the motion equation yields
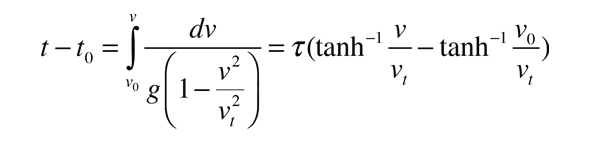
which expresses the fall time t in terms of the characteristic time for the motion
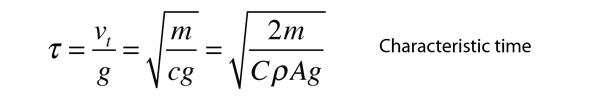
The motion equation can then be solved for the velocity v:

If the falling object was released from rest at time t=0, the velocity expression becomes:
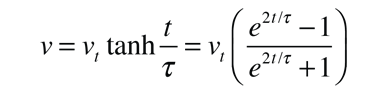
The nature of the motion is such that the speed is essentially at its terminal velocity vt after a few characteristic times. At t = 5τ, the speed is 0.99991 vt.
Freefall Distance as a Function of Time
The distance of freefall y as a function of time may be obtained by integrating the velocity expression above.

The form of this integral is
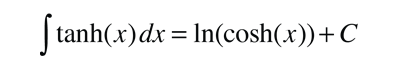
The constant of integration C=0 because cosh(0)=1 and ln(1)=0, so the result of the integration is

Time of impact upon falling from peak height
If we substitute the peak height ypeak into the distance equation above so that it has reached the surface from which it was launched, we obtain the relationship

Taking the exponential of both sides gives
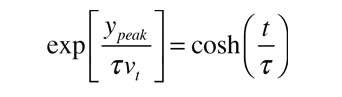
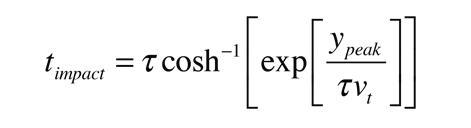
This expression is used in the vertical trajectory calculation.
Fluid friction
Reference
Fowles & Cassiday
Sec. 2.4
| HyperPhysics***** Mechanics ***** Fluids | R Nave |