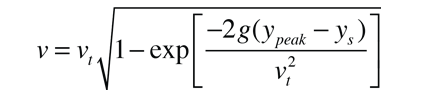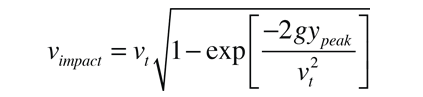Freefall Velocity vs Distance for Quadratic Drag

A freely falling object will be presumed to experience an air resistance force proportional to the square of its speed. The downward direction will be taken as positive, and the velocity as a function of distance y for an object dropped from rest is the object of the calculation. The expressions will be developed for the two forms of air drag which will be used for trajectories

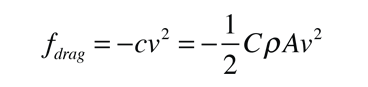
The freefall velocity as a function of time if dropped from rest is given by

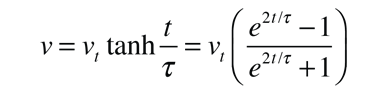
This equation may be converted to one in which the independent variable is distance instead of time by making use of the expression

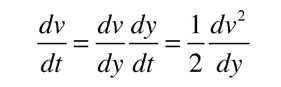
This can be used to rewrite the motion equation above as

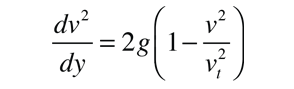
This equation is solved by the following procedure:

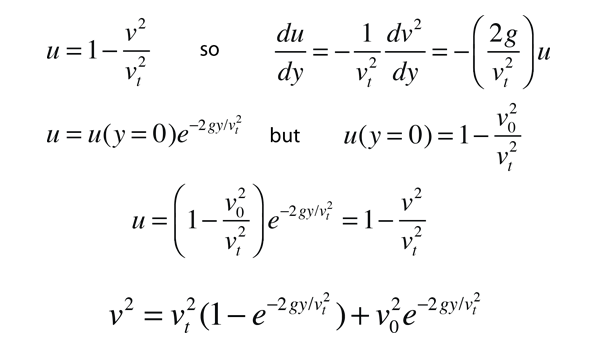
This expresses the freefall velocity v in terms of the fall distance y. It has two exponential decay terms so that after a sufficient fall distance, the velocity is essentially the terminal velocity v_t. A characteristic length v_t²/2g expresses a distance where the velocity approaches v_t.

Freefall Velocity vs Height for Quadratic Drag

A freely falling object will be presumed to experience an air resistance force proportional to the square of its speed. The downward direction will be taken as positive, and the velocity as a function of the height y_s for an object dropped from a peak height y_peak is the object of the calculation. Note that y_s is being used as the height above the surface in this case, so it is not the same as the y in the above development. From that development above, the velocity as a function of the distance of fall from the peak height is given by

where y = y_peak - y_s. For this application v₀=0 since the velocity is zero at the peak height. The expression for v then becomes

The velocity at impact can then be obtained for y_s=0:

These expressions are used in the vertical trajectory calculation.