|
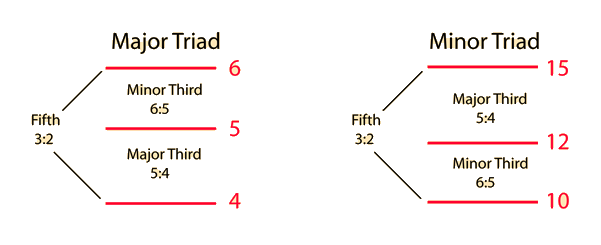
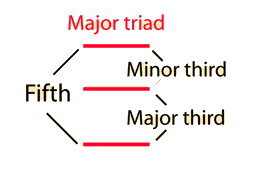
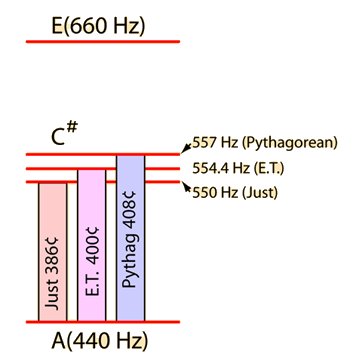
Harmonic Intervals in CentsExpressing the musical intervals between successive harmonics in cents notation helps to show the relationship between the harmonics and the equal tempered musical scale. The equal tempered intervals are all in multiples of 100 cents, so the departure from such a multiple is an indication of how much the just interval is out of tune with equal temperament. If any musical source produces a fundamental and a series of exact harmonices, then it is evident that the upper harmonics will be out of tune with the corresponding equal tempered notes. Examination of the illustration will make it evident that the 7th harmonic shows the most severe departure from any equal tempered interval. This is important in the design of brass instruments, since they use the upper resonances of the instrument as played notes in a harmonic sequence. Fortunately, the upper resonances of brass instruments can be tuned closer to equal temperament in the manufacturing process so that the problem is not so severe, but the seventh resonance is still troublesome. |
Temperament and musical scales
| HyperPhysics***** Sound | R Nave |