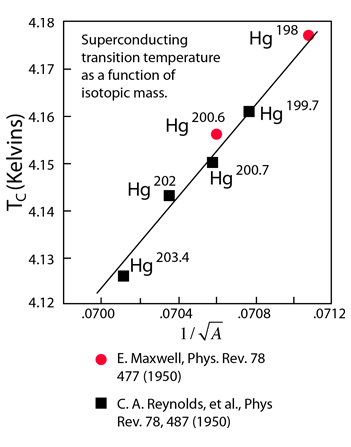
Isotope Effect, Mercury
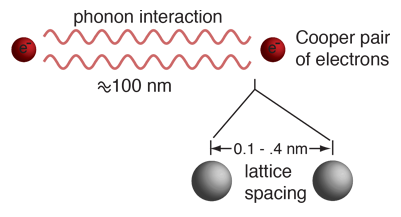
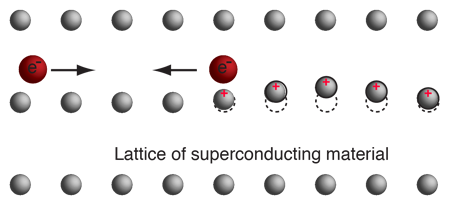
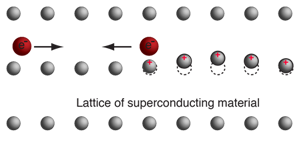
If electrical conduction in mercury were purely electronic, there should be no dependence upon the nuclear masses. This dependence of the critical temperature for superconductivity upon isotopic mass was the first direct evidence for interaction between the electrons and the lattice. This supported the BCS theory of lattice coupling of electron pairs.
|
It is quite remarkable that an electrical phenomenon like the transition to zero resistivity should involve a purely mechanical property of the lattice. Since a change in the critical temperature involves a change in the energy environment associated with the superconducting transition, this suggests that part of the energy is being used to move the atoms of the lattice since the energy depends upon the mass of the lattice. This indicates that lattice vibrations are a part of the superconducting process. This was an important clue in the process of developing the BCS theory because it suggested lattice coupling, and in the quantum treatment suggested that phonons were involved.
|
|
Index
Superconductivity concepts
Reference Rohlf,Ch 15 |