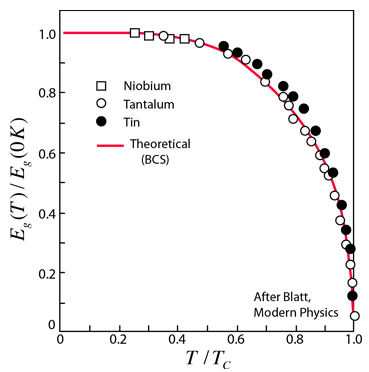
Measured Superconductor Bandgap
 |
The measured bandgap in Type I superconductors is one of the pieces of experimental evidence which supports the BCS theory. The BCS theory predicts a bandgap of 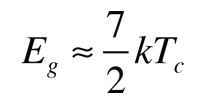 where Tc is the critical temperature for the superconductor. The energy gap is related to the coherence length for the superconductor, one of the two characteristic lengths associated with superconductivity.
|
Superconductivity concepts
Reference Rohlf,Ch 15
| HyperPhysics***** Condensed Matter | R Nave |