Entropy as a Measure of the Multiplicity of a System
The probability of finding a system in a given state depends upon the multiplicity of that state. That is to say, it is proportional to the number of ways you can produce that state. Here a "state" is defined by some measurable property which would allow you to distinguish it from other states. In throwing a pair of dice, that measurable property is the sum of the number of dots facing up. The multiplicity for two dots showing is just one, because there is only one arrangement of the dice which will give that state. The multiplicity for seven dots showing is six, because there are six arrangements of the dice which will show a total of seven dots.
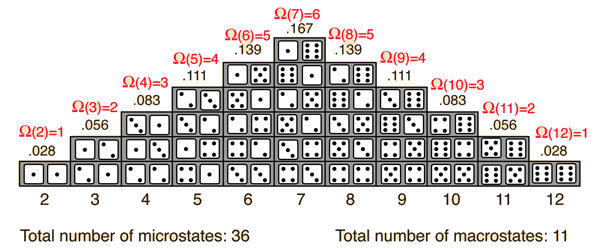
One way to define the quantity "entropy" is to do it in terms of the multiplicity.
where k is Boltzmann's constant. This is Boltzmann's expression for entropy, and in fact S = klnΩ is carved onto his tombstone! (Actually, S = klnW is there, but the Ω is typically used in current texts (see Wikipedia)).The k is included as part of the historical definition of entropy and gives the units joule/kelvin in the SI system of units. The logarithm is used to make the defined entropy of reasonable size. It also gives the right kind of behavior for combining two systems. The entropy of the combined systems will be the sum of their entropies, but the multiplicity will be the product of their multiplicities. The fact that the logarithm of the product of two multiplicities is the sum of their individual logarithms gives the proper kind of combination of entropies. The multiplicity for ordinary collections of matter is inconveniently large, on the order of Avogadro's number, so using the logarithm of the multiplicity as entropy is convenient.
For a system of a large number of particles, like a mole of atoms, the most probable state will be overwhelmingly probable. You can with confidence expect that the system at equilibrium will be found in the state of highest multiplicity since fluctuations from that state will usually be too small to measure. As a large system approaches equilibrium, its multiplicity (entropy) tends to increase. This is a way of stating the second law of thermodynamics.
Entropy concepts
Reference
Schroeder
Ch 2
| HyperPhysics***** Thermodynamics | R Nave |