Entropy of an Ideal Gas
The entropy S of a monoatomic ideal gas can be expressed in a famous equation called the Sackur-Tetrode equation.
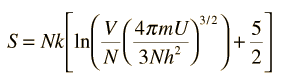
where
- N = number of atoms
- k = Boltzmann's constant
- V = volume
- U = internal energy
- h = Planck's constant
One of the things which can be determined directly from this equation is the change in entropy during an isothermal expansion where N and U are constant (implying Q=W). Expanding the entropy expression for Vf and Vi with log combination rules leads to
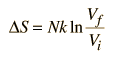
For determining other functions, it is useful to expand the entropy expression using the logarithm of products to separate the U and V dependence.
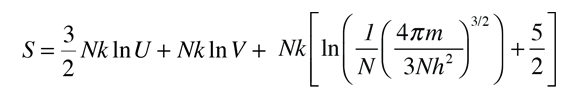
Then making use of the definition of temperature in terms of entropy:

This gives an expression for internal energy that is consistent with equipartition of energy.
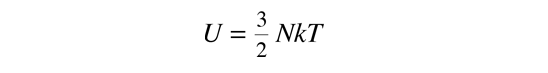
with kT/2 of energy for each degree of freedom for each atom.
For processes with an ideal gas, the change in entropy can be calculated from the relationship
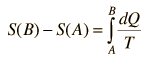
Making use of the first law of thermodynamics and the nature of system work, this can be written
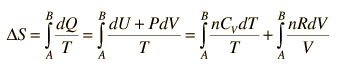
 |
|
This is a useful calculation form if the temperatures and volumes are known, but if you are working on a PV diagram it is preferable to have it expressed in those terms. Using the ideal gas law
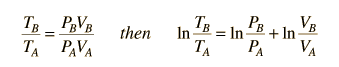
then
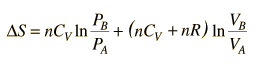 .
.But since specific heats are related by CP = CV + R,
 .
.Since entropy is a state variable, just depending upon the beginning and end states, these expressions can be used for any two points that can be put on one of the standard graphs.
Entropy concepts
Reference
Schroeder
Ch 2
| HyperPhysics***** Thermodynamics | R Nave |