Relation of Electric Field to Charge Density
Since electric charge is the source of electric field, the electric field at any point in space can be mathematically related to the charges present. The simplest example is that of an isolated point charge. For multiple point charges, a vector sum of point charge fields is required. If we envision a continuous distribution of charge, then calculus is required and things can become very complex mathematically.
One approach to continuous charge distributions is to define electric flux and make use of Gauss' law to relate the electric field at a surface to the total charge enclosed within the surface. This involves integration of the flux over the surface.
Another approach is to relate derivatives of the electric field to the charge density. This approach can be considered to arise from one of Maxwell's equations and involves the vector calculus operation called the divergence. The divergence of the electric field at a point in space is equal to the charge density divided by the permittivity of space.

In a charge-free region of space where r = 0, we can say
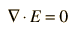
While these relationships could be used to calculate the electric field produced by a given charge distribution, the fact that E is a vector quantity increases the complexity of that calculation. It is often more practical to convert this relationship into one which relates the scalar electric potential to the charge density. This gives Poisson's equation and LaPlace's equation.
Electric field concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |