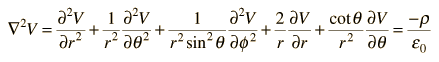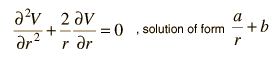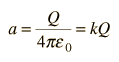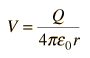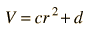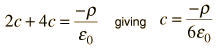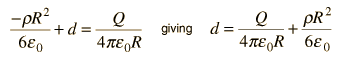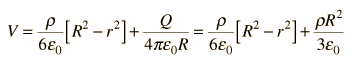LaPlace's and Poisson's Equations
A useful approach to the calculation of electric potentials is to relate that potential to the charge density which gives rise to it. The electric field is related to the charge density by the divergence relationship
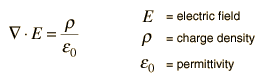
and the electric field is related to the electric potential by a gradient relationship
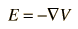
Therefore the potential is related to the charge density by Poisson's equation

In a charge-free region of space, this becomes LaPlace's equation

This mathematical operation, the divergence of the gradient of a function, is called the LaPlacian. Expressing the LaPlacian in different coordinate systems to take advantage of the symmetry of a charge distribution helps in the solution for the electric potential V. For example, if the charge distribution has spherical symmetry, you use the LaPlacian in spherical polar coordinates.
Since the potential is a scalar function, this approach has advantages over trying to calculate the electric field directly. Once the potential has been calculated, the electric field can be computed by taking the gradient of the potential.
| Example: sphere of uniform charge |
Electric field concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |