Skin Effect in AC Conduction

For Direct Current through a wire, the resistance of the wire can be calculated from its length, diameter and resistivity since it may be assumed that the electric current is essentially uniform over the cross-section of the wire. However, for Alternating Current, the interaction of electric and magnetic fields in the conductor distribute the current preferentially to the outside of the wire. This skin effect increases with frequency so that for high Radio Frequencies (RF) a thin outside layer of the conductor carries essentially all the current.

The AC current density J drops exponentially from the outside radius in a way that can be quantified in terms of a parameter called the "skin depth" δ:

where J_S is the current density at the surface and d is the depth beneath the surface. The skin depth δ can be calculated from:

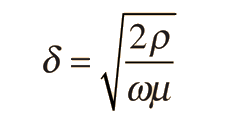where ρ = electrical resistivity ω = angular frequency = 2π f μ = magnetic permeability

Frequency Skin depth δ in μm Skin depth δ in mm 60 Hz 8470 8.47 10 kHz 660 0.66 100 kHz 210 0.21 1 MHz 66 0.066 10MHz 21 0.021 100 MHz 6.6 0.0066

The skin effect becomes a major consideration in RF circuits. From the exponential nature of the drop in current density, you can show that 63% of the current will flow within one skin depth δ of the surface and 98% will flow within 4δ of the surface. For frequencies above 100MHz it is wasteful of conductive metals to use solid conductors, so multiconductor straps or tubing can be used to utilize the larger surface areas.

References:

RadioWorld

ecee.colorado

Blank