Vergence

The vergence of light is defined by

Vergence = V = n/L

where n is the index of refraction of the medium and L is the distance in accordance with the Cartesian sign convention. The standard use of vergence expresses the distance L in meters, so the unit of vergence is m-1, often called "diopters".

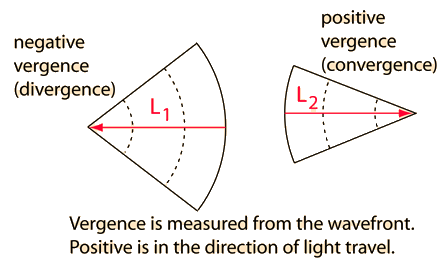Since the distance L1 is measured from the wavefront and light is traveling left to right, it is a negative distance and the vergence is negative (divergent). L2 is positive since it is directed to the right from the wavefront (convergent).

The change in vergence when the light encounters a refracting surface is equal to the power of the surface Ps:

V + Ps = V'
Vergence ExampleVergence Tracing in Thick Lenses
 Index

Lens concepts

Thick lens concepts

Meyer-Arendt
Ch 1.1
 
HyperPhysics***** Light and Vision R Nave
 Go Back










Vergence Example

The example below shows a positive lens followed by a negative one, but the powers can be given any value, positive or negative. At each surface the relationship V + Ps = V' is applied, and the change in vergence between surfaces is calculated.

This calculation will make use of the surface powers of the lenses, their indices of refraction and thickness, and the separation of the lenses. Note that the vertical displacements of the indicated light path are greatly exaggerated since the application of vergence tracing for thick lenses is limited to the small angles of paraxial rays.

A default set of values for the parameters of this calculation is provided. You can see the default calculation by entering a 0 into one of the lens parameters, which will trigger the entry of the default parameters for the lenses. Any of them may be then changed to explore the behavior of the lens system.

Lens 1:
n1 = , P1=, P2=, thickness t1 =

Lens 2:
n2 = , P3=, P4=, thickness t2 =

Lens separation d =

The vergences can be calculated from the lens parameters and the object distance.The change in vergence when the light encounters a refracting surface is equal to the power of the surface:

Using the Cartesian sign convention, the object distance is typically a negative number since it points opposite to the direction of light travel.

Object distance o = m.

The vergences can then be calculated.

V1 = n0/o = m-1

V11 = vergence inside Lens 1 = V1 + P1 = n1/i1 = m-1
where i1 = intermediate image distance if formed by P1 alone inside medium of index n1.

V12 = vergence before exiting Lens 1 = n1/(i1 - t 1) = m-1

V2 = n1/(i1 - t 1) +P2 = 1/i2 =m-1
where i2 is the projected image distance upon exit from Lens 1.

V3 = 1/(i2 - d) = m-1

V31 = vergence just inside Lens 2 = V3 + P3 = n2/i3 = m-1
where i3 is the projected image distance if formed within the second lens medium.

V32 = vergence before exiting Lens 2 = n2/(i3 - t 2) = m-1.

V4 = n2/(i3 - t 2) + P4 = 1/i =m-1
Where i is the image distance measured from the final surface.

The values i1, i2, and i3 are calculated as intermediate values above would be the image distances inside the glass with just the most recent surface power acting. This calculation presumes that these image distances are greater than the thickness of the lenses in which they are calculated, and that may not be true for the lens parameters chosen. It is also presumed that the medium is air so that n0 = 1.

The exit vergence from the final surface determines the image distance with respect to that surface.

Image distance i = 1/V4 = m.

Compare to solution by matrix method
Vergence Tracing in Thick Lenses
 Index

Lens concepts

Thick lens concepts
 
HyperPhysics***** Light and Vision R Nave
 Go Back