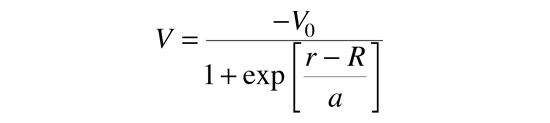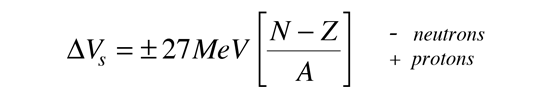Shell Model of Nucleus
Visualizing the densely packed nucleus in terms of orbits and shells seems much less plausible than the corresponding shell model for atomic electrons. You can easily believe that an atomic electron can complete many orbits without running into anything, but you expect protons and neutrons in a nucleus to be in a continuous process of collision with each other. But dense-gas type models of nuclei with multiple collisions between particles didn't fit the data, and remarkable patterns like the "magic numbers" in the stability of nuclei suggested the seemingly improbable shell structure.
With the enormous strong force acting between them and with so many nucleons to collide with, how can nucleons possibly complete whole orbits without interacting? This has the marks of a Pauli exclusion principle process, where two fermions cannot occupy the same quantum state. If there are no nearby, unfilled quantum states that are in reach of the available energy for an interaction, then the interaction will not occur. This is essentially a quantum idea - if there is not an available "hole" for a collision to knock a nucleon into, then the collision will not occur. There is no classical analog to this situation.
The evidence for a kind of shell structure and a limited number of allowed energy states suggests that a nucleon moves in some kind of effective potential well created by the forces of all the other nucleons. This leads to energy quantization in a manner similar to the square well and harmonic oscillator potentials. Since the details of the well determine the energies, much effort has gone into construction of potential wells for the modeling of the observed nuclear energy levels. Solving for the energies from such potentials gives a series of energy levels like that at left below. The labels on the levels are somewhat different from the corresponding symbols for atomic energy levels. The energy levels increase with orbital angular momentum quantum number l, and the s,p,d,f... symbols are used for l=0,1,2,3... just like the atomic case. But there is really no physical analog to the principal quantum number n, so the numbers associated with the level just start at n=1 for the lowest level associated with a given orbital quantum number, giving such symbols as 1g which could not occur in the atomic labeling scheme. The quantum number for orbital angular momentum is not limited to n as in the atomic case.
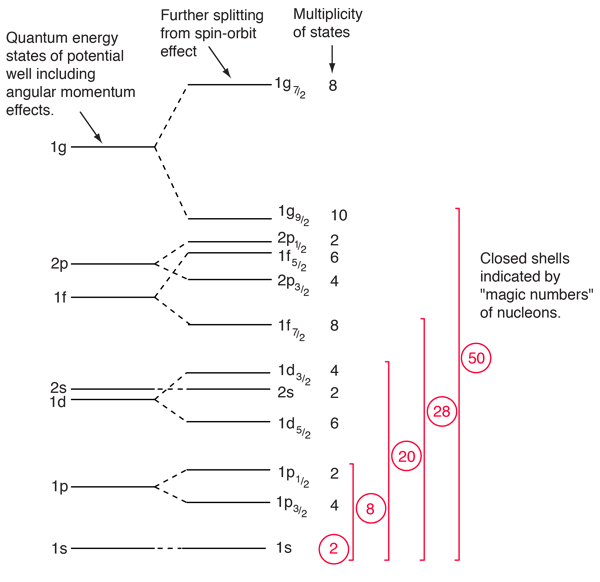
In addition to the dependence on the details of the potential well and the orbital quantum number, there is a sizable spin-orbit interaction which splits the levels by an amount which increases with orbital quantum number. This leads to the overlapping levels as shown in the illustration. The subscript indicates the value of the total angular momentum j, and the multiplicity of the state is 2j + 1. The contribution of a proton to the energy is somewhat different from that of a neutron because of the coulomb repulsion, but it makes little difference in the appearance of the set of energy levels.
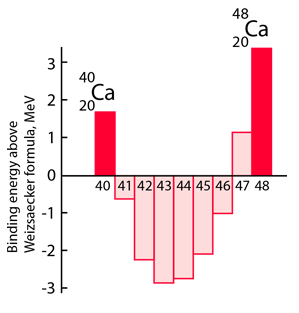
With this set of identified nuclear states and the magic numbers, we can predict the net nuclear spin of a nucleus and represent it's nuclear state based on the identification of the level of the odd nucleon in the order of states shown above. The parity of the state can also be predicted, so the single particle shell model has shown itself to be of significant benefit in characterizing nuclei.
| "Magic numbers" of nucleons | Nuclear potential wells | Nuclear spectra |
| Energy level notation | Spherical potential well |
Nuclear Structure Concepts
References
Cohen
Concepts of Nuclear Physics, Ch 4
Rohlf
Sec 11.3
Das & Ferbel
Ch. 3
| HyperPhysics***** Nuclear | R Nave |