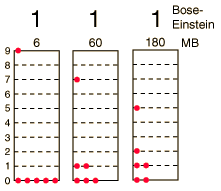
Show all 26 possible distributions

How many ways can you distribute 9 units of energy among 6 identical, indistinguishable bosons?

The three distributions of particles at left each have the same energy, the same kind of particles, and the same number of particles. If the particles were distinguishable particles and described by Maxwell-Boltzmann statistics, then the distribution at right would be 30 times more likely than the one on the left because there are 30x as many distinguishable ways to produce it. But if they are indistinguishable bosons, the three states are equally probable and given a statistical weight of 1. This means that instead of 2002 distinguishable microstates arising from 26 macrostates, there are only 26 states.

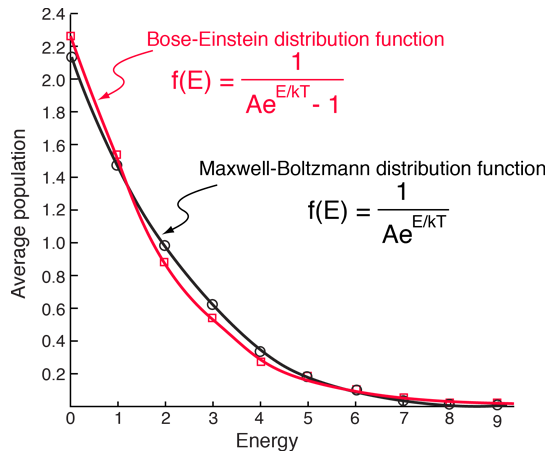
Evaluating the average occupancy of each energy state is much simpler than in the Maxwell-Boltzmann example since each macrostate has a weight of 1. The average occupancy is just the sum of the numbers of particles in a given energy state over all the 26 distributions divided by 26.

Evaluate the average for each energy state.Compare with Maxwell-Boltzmann example.
 Index

Reference
Blatt
Ch. 11
 
HyperPhysics***** Quantum Physics R Nave
 Go Back





The average distribution of 9 units of energy among 6 identical particles

Energy
level		Average
number
Maxwell-
Boltzmann		Average
number
Bose-
Einstein
0
2.143
2.269
1
1.484
1.538
2
0.989
0.885
3
0.629
0.538
4
0.378
0.269
5
0.210
0.192
6
0.105
0.115
7
0.045
0.077
8
0.015
0.038
9
0.003
0.038

There are 26 possible distributions of 9 units of energy among 6 particles, and if those particles are indistinguishable and described by Bose-Einstein statistics, all of the distributions have equal probability. To get a distribution function of the number of particles as a function of energy, the average population of each energy state must be taken. The average for each of the 9 states is shown below compared to the result obtained by Maxwell-Boltzmann statistics.

Low energy states are more probable with Bose-Einstein statistics than with the Maxwell-Boltzmann statistics. While that excess is not dramatic in this example for a small number of particles, it becomes very dramatic with large numbers and low temperatures. At very low temperatures, bosons can "condense" into the lowest energy state. The phenomenon called Bose-Einstein condensation is observed with liquid helium and is responsible for its remarkable behavior.

Compare with Fermi-Dirac example.Compare with Maxwell-Boltzmann example.
 Index

Reference
Blatt
Ch. 11
 
HyperPhysics***** Quantum Physics R Nave
 Go Back