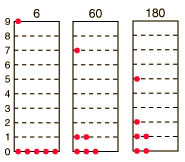
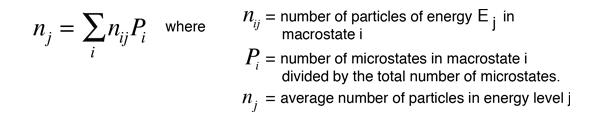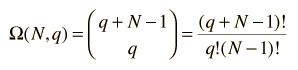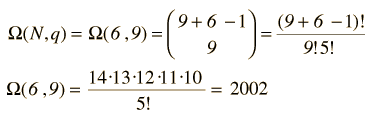 |
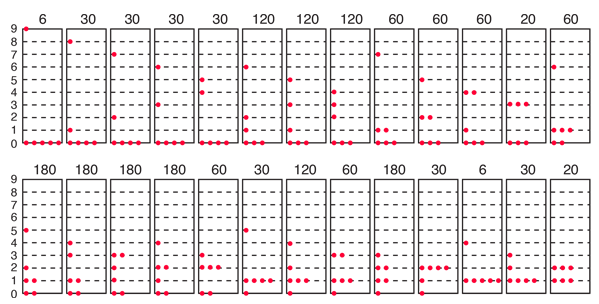
How many ways can you distribute 9 units of energy among 6 identical particles?
The three distributions of particles at left each have the same energy, the same kind of particles, and the same number of particles, yet the distribution at the right is 30 times more likely than the one at the left. Why is this? For the distinguishable particles which are presumed by the Maxwell-Boltzmann distribution, it matters not only how many particles are in each state, but which particles are in each state.
|
Blatt uses the term "macrostate" to describe the characterization of the system which gives just the number of particles in each state; the diagram above shows three of the 26 possible macrostates for this system. The term "microstate" is used for the more detailed characterization in which the specific energy level for each particle is given. The macrostate at left has only 6 microstates, because there are only 6 ways to put one particle in level 9 and the other 5 in level 0. But there are 180 ways to achieve the macrostate at right, so if every distribution is presumed to be equally likely, then the system is 30 times more likely to be found in the right hand macrostate.
The number of distinguishable ways to produce each distribution is given by

So for the three macrostates pictured above, the numbers of microstates are

(Recall that 0!=1 so that the unoccupied states do not affect the calculation.)
Now to establish the distribution function for the number of particles in each energy state, the number of particles in each state must be averaged over all of the microstates. For each macrostate, the number of particles in a given energy level is multiplied by the number of microstates. The sum of those products is divided by the total number of microstates, which is 2002 in this case.
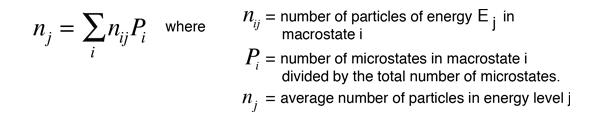
The number of microstates (the multiplicity W) for q units of energy among N equally probable states can be mathematically evaluated from the expression
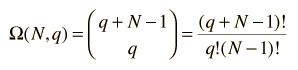
which for this case becomes
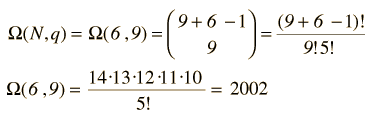
|
Index
Reference
Blatt
Ch. 11 |