BCS Theory of Superconductivity

The properties of Type I superconductors were modeled successfully by the efforts of John Bardeen, Leon Cooper, and Robert Schrieffer in what is commonly called the BCS theory. A key conceptual element in this theory is the pairing of electrons close to the Fermi level into Cooper pairs through interaction with the crystal lattice. This pairing results from a slight attraction between the electrons related to lattice vibrations; the coupling to the lattice is called a phonon interaction.

Pairs of electrons can behave very differently from single electrons which are fermions and must obey the Pauli exclusion principle. The pairs of electrons act more like bosons which can condense into the same energy level. The electron pairs have a slightly lower energy and leave an energy gap above them on the order of .001 eV which inhibits the kind of collision interactions which lead to ordinary resistivity. For temperatures such that the thermal energy is less than the band gap, the material exhibits zero resistivity.

Bardeen, Cooper, and Schrieffer received the Nobel Prize in 1972 for the development of the theory of superconductivity.

Experimental Support: BCS Theory

Electrons acting as pairs via lattice interaction? How did they come up with that idea for the BCS theory of superconductivity? The evidence for a small band gap at the Fermi level was a key piece in the puzzle. That evidence comes from the existence of a critical temperature, the existence of a critical magnetic field, and the exponential nature of the heat capacity variation in the Type I superconductors.

The evidence for interaction with the crystal lattice came first from the isotope effect on the critical temperature.

The band gap suggested a phase transition in which there was a kind of condensation, like a Bose-Einstein condensation, but electrons alone cannot condense into the same energy level (Pauli exclusion principle). Yet a drastic change in conductivity demanded a drastic change in electron behavior. Perhaps coupled pairs of electrons with antiparallel spins could act like bosons?

Measured Superconductor Bandgap

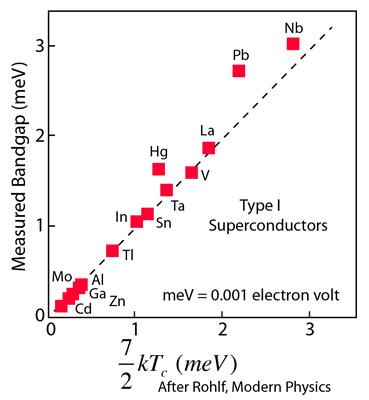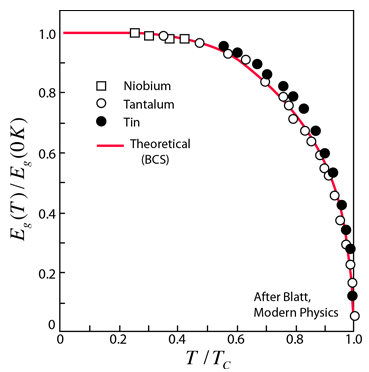
The measured bandgap in Type I superconductors is one of the pieces of experimental evidence which supports the BCS theory. The BCS theory predicts a bandgap of 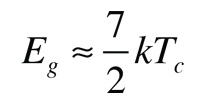where Tc is the critical temperature for the superconductor. The energy gap is related to the coherence length for the superconductor, one of the two characteristic lengths associated with superconductivity. Energy gap variations with temperature

Energy Gap in Superconductors as a Function of Temperature

The effective energy gap in superconductors can be measured in microwave absorption experiments. The data at left offer general confirmation of the BCS theory of superconductivity. The data is attributed to Townsend and Sutton.

The reduction of the energy gap as you approach the critical temperature can be taken as an indication that the charge carriers have some sort of collective nature. That is, the charge carriers must consist of at least two things which are bound together, and the binding energy is weakening as you approach the critical temperature. Above the critical temperature, such collections do not exist, and normal resistivity prevails. This kind of evidence, along with the isotope effect which showed that the crystal lattice was involved, helped to suggest the picture of paired electrons bound together by phonon interactions with the lattice.

Vanadium Heat Capacity

The heat capacity of superconducting vanadium is very different from that of vanadium which is kept in the normal state by imposing a magnetic field on the sample. The exponential increase in heat capacity near the critical temperature suggests an energy bandgap for the superconducting material. This evidence for a bandgap is one of the pieces of experimental evidence which supports the BCS theory of superconductivity.

Exponential Heat Capacity

As it is warmed toward its critical temperature, the heat capacity of vanadium increases 100-fold in just 4 K. This exponential increase suggests an energy gap which must be bridged by thermal energy. This energy gap evidence was part of the experimental motivation for the BCS theory of superconductivity.

From comparisons with other methods of determining the band gap, it is found that the constant "b" in the exponential heat capacity expression is one-half the band gap energy. If the slope of the line in the illustration is determined by scaling, it is about b=7.4k, corresponding to an energy gap of about 1.3 meV. This is slightly lower than the value obtained by other methods. The value predicted for vanadium from its critical temperature of 5.38 K by the BCS theory is 1.6 meV, and the measured value is close to that.

Compare heat capacity of normal and superconducting vanadium. Data from W. S. Korak, et al., Phys. Rev. 102, 656 (1956)