Infrared Ear Thermometer
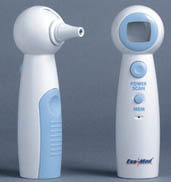  |
Body temperature is routinely monitored in clinical settings with infrared ear thermometers which measure the infrared energy emitted from the patient's eardrum in a calibrated length of time. A short tube with a protective sleeve is inserted into the ear, and a shutter is opened to allow radiation from the tympanic membrane to fall on an infrared detector for a period which is typically from 0.1 to 0.3 seconds in the varieties surveyed. The device beeps when data collection is completed and a readout of temperature is produced on a liquid crystal display. This kind of temperature from the eardrum has been found to be a clinically reliable indicator of body core temperature. The eardrum is located close to the hypothalmus, which is the body's temperature regulator. The membrane itself is thin and almost transparent in the visible, so you would presume that it reliably tracks the temperature inside the membrane so that the infrared energy it emits gives a good indication of the inside temperature. The infrared energy falls on a thin pyroelectric crystal which develops a charge proportional to that collected energy. Discharging the crystal sends a current pulse through filters and conversion circuits which compare the signal to tabulated data on temperature and calculate a body temperature for the display. |
All objects above absolute zero temperature emit radiation, and the radiation from an isolated object at body temperature has a characteristic wavelength dependence given by the blackbody radiation curve. For a body temperature of 37°C this radiation curve peaks at a wavelength of about 9340 nm in the infrared, compared to the visible wavelength range of 400-700 nm. This peak can be determined from the Wien displacement law. Presuming that the pyroelectric detector develops an electric charge proportional to the energy which falls on it during the collection time, the energy discrimination necessary for a given accuracy could be calculated using the Stefan-Boltzmann law which relates radiated energy to temperature. The ratio of the radiated energy with 1°C fever would be [(38 +273)/(37 + 273)]4 = 1.013 since the radiated energy is proportional to the fourth power of the absolute temperature. You would then have to achieve a resolution of 1.3% or better to detect that temperature difference. The devices claim to have a temperature resolution of 0.1°F, which requires a resolution of 0.07% in the measurement of the radiated energy.
Not having access to the details of the detector, I would guess that the detectors use an infrared wavelength window on the steep part of the blackbody curve and make use of the fact that the blackbody curve shifts downward in wavelength as well as upward in total intensity as the temperature rises. This could give an enhanced change in radiation through the window of the detector so that the absolute resolution doesn't have to be as high. For example, the radiation through a certain wavelength window can be calculated for 37 °C and compared with that at another temperature. At 37 °C the radiated intensity peak is at 9344 nm from the Wien law. If you choose a 500 nm window at 5500 nm, the radiated intensity is about half that, but the change in power through a window from 5500 to 6000 nm changes by 0.15% when you increase the temperature by 0.1°F, a sensitivity twice that quoted above.
Temperature concepts
| HyperPhysics***** Thermodynamics | R Nave |