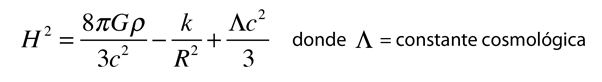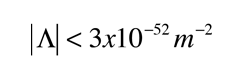La Ecuación de Friedmann
A Alexander Friedmann de Rusia se le acredita el desarrollo de una ecuación dinámica de la expansión del universo en 1920. Este fue un momento en que Einstein, Willem de Sitter de los Países Bajos, y Georges Lemaitre de Francia, también estaban trabajando en ecuaciones para modelar el universo. Friedmann lo desarrolló como una ecuación relativista en el marco de la relatividad general, pero la descripción aquí se limita a una versión no relativista simplificada, basada en las leyes de Newton.
Las formas convenientes de la ecuación de Friedmann con el que examinar la temperatura y el tiempo de expansión para el modelo del Big Bang del universo son
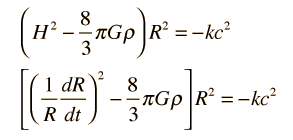
Además de la densidad y la constante de gravitación G, la ecuación contiene el parámetro de Hubble H, un parámetro de escala R, y un factor k que se llama parámetro de curvatura. El parámetro de curvatura indica si el universo es abierto o cerrado. Las ecuaciones anteriores no especifican la naturaleza de la densidad ρ. No incluyen las posibles interacciones de partículas que no sean la atracción gravitatoria. Tales interacciones de partículas como las colisiones, podrían especificarse en términos de presión, por lo que al modelo anterior se le refiere a veces como un universo "sin presión". Las versiones más detalladas de la ecuación de Friedman incluyen tales efectos.
Einstein consideró agregar un nuevo término, la famosa (o infame) constante cosmológica que produciría un universo estático.
| Relacionar con Temperatura y Tiempo de Expansión |
Referencias
Rohlf
Cap. 19
Kaufmann
Cap. 28
| HyperPhysics*****Astrofísica | M Olmo R Nave |