División de la Energía entre los Fotones y las Partículas Masivas
Una de las ideas asociadas con el modelado del Big Bang es, que cuanto más atrás se proyecta en el tiempo, más dominado por los fotones está el universo. Pensamos que el universo actual es sobre todo materia, pero la energía del universo primitivo era principalmente energía de fotones, con partículas masivas jugando un papel muy pequeño.
La cantidad de energía de radiación en el universo de hoy puede ser estimada con el uso de la ley de Stefan-Boltzmann, teniendo en cuenta que el universo está lleno de radiación de cuerpo negro a una temperatura de 2,7 K. La densidad de energía en esta radiación de equilibrio está dada por

También hay una energía de fondo en los neutrinos, que se espera que tengan una temperatura de aproximadamente 1,9 K, y de acuerdo con el modelo estándar hay 7/4 de ellos con relación al número de fotones. Tratándolos como partículas sin masa daría una densidad de energía de aproximadamente 0,11 MeV/m3, por lo que la densidad total de energía de los fotones y los neutrinos es aproximadamente
 |
|
Una estimación actual de la cantidad de masa en el universo actual es
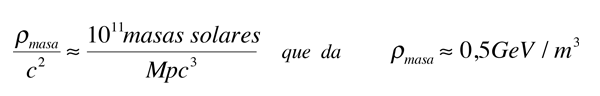
por lo que las estimaciones actuales, coloca la cantidad de energía en partículas masivas, como más de mil veces mayor que la energía en radiación.
| Relacionar con Temperatura y Tiempo de Expansión |
Referencia
Rohlf
Cap. 19
| HyperPhysics*****Astrofísica | M Olmo R Nave |
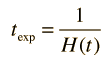 ,
,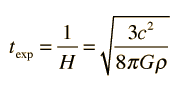 .
. .
. .
. .
. .
. .
.