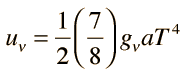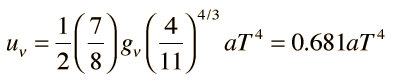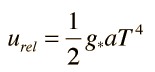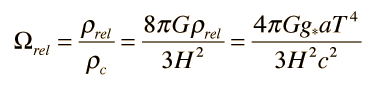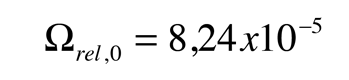Energía de Radiación en el Universo Primitivo
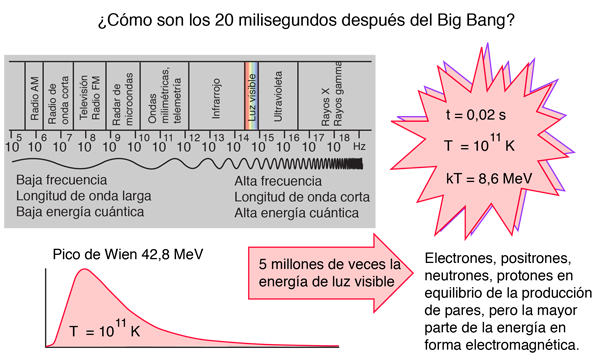
La radiación electromagnética y el flujo de neutrinos eran la forma dominante de energía en el universo primitivo, siendo más dominante cuanto mas atrás vayamos en el modelo del Big Bang. Es una reminiscencia de la frase bíblica "Sea la luz". Pero por supuesto, esto no es luz visible sino rayos gamma, puesto que la energía de fotón promedio aumenta, según se va atrás en el tiempo y eran lo suficientemente altas para lograr la producción de pares de todas las partículas conocidas. Por ejemplo, a la temperatura de 1011 K, que corresponde al tiempo de alrededor de los 20 milisegundos del modelo de Weinberg del big bang, la energía térmica era kT = 8,6 MeV. A esta temperatura, el pico de energía dada por la ley de desplazamiento de Wien es de 42,8 MeV. La energía de la radiación era suficiente, no sólo para la producción de pares electrón-positrón, sino también para mantener poblaciones esencialmente iguales de protones y neutrones. Así que en esa época, la radiación fue verdaderamente dominante.
La densidad de energía de radiación en los textos de astronomía se pone generalmente en la forma
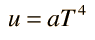
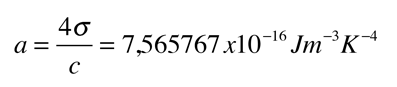
Por coherencia con otras cantidades de partículas que se expresan en términos del número de grados de libertad, esto se escribe a veces en la forma

Para evaluar el papel de la radiación en la expansión del universo primitivo, hay que dar un paso más allá del sencillo modelo de expansión newtoniano e incluir la presión de radiación. Cuando se incluye la presión de la radiación, la densidad efectiva representada por la radiación como función del factor de escala R es
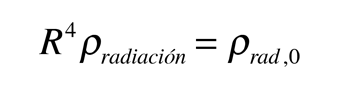
La dependencia de la cuarta potencia de R distingue la densidad de energía de radiación de la densidad de masa, la cual depende de la tercera potencia de R,
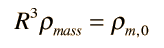
| La Materia y la Radiación en el Universo Primitivo |
| ¿Qué Edad tiene el Universo? |
Referencia
Carroll & Ostlie
Cap.29
| HyperPhysics*****Astrofísica | M Olmo R Nave |