Modelo Newtoniano de la Expansión del Universo
Ahora es un hecho experimental que el universo se está expandiendo, y expandiéndose a una tasa muy cercana a la que haría que el universo fuese "plano" o "crítico", con lo que se expandiría para siempre, aproximándose asintóticamente a una condición de reposo en un tiempo infinito. En realidad, la información actual indica una pequeña aceleración atribuida a la energía oscura, pero aún lo suficientemente cerca de la densidad crítica, que tiene sentido modelar un universo plano o crítico. A tal fin, se puede modelar la expansión en términos de una densidad uniforme de partículas que interactúan sólo gravitacionalmente, para crear un marco de trabajo desde el cual desarrollar modelos más refinados. Esos modelos más refinados se expresan a menudo en la ecuación de Friedman.
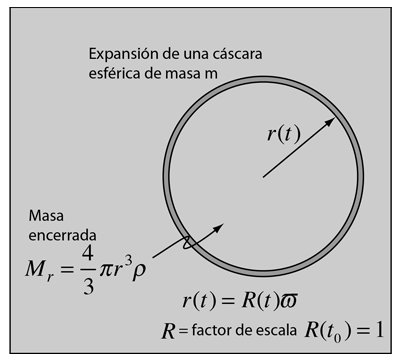 |
Una carcasa esférica de masa m que se está expandiendo, puede ser descrita en términos de su energía cinética, y su energía potencial gravitatoria debida a la masa Mr, encerrada en la esfera. A la carcasa esférica de masa se le ha dado una energía E. |
La energía mecánica se puede expresar de la siguiente manera, usando la notación de Carroll y Ostlie:
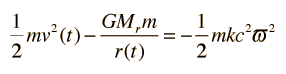
El término de la derecha es una expresión de la energía total de la carcasa, que se ha construido de forma que pueda tener utilidad en el futuro. En esa expresión, c es la velocidad de la luz, m es la masa, k es una constante que se usa para representar la "curvatura" del sistema espacial, y ϖ es una coordenada cuyo valor representa la carcasa de masa elegida, y permanecerá constante como una "coordenada comóvil" para especificar esa carcasa. El radio r(t) se puede expresar en términos de un factor de escala dependiente del tiempo R(t) que especifica la expansión del espacio y esta coordenada comóvil:

Ahora, haciendo uso de la ley de Hubble, se puede expresar la velocidad de la carcasa en expansión como
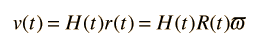
Como la velocidad también puede expresarse como
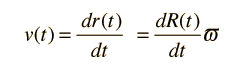
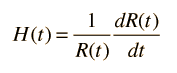
Ahora bien, estos términos pueden ser sustituidos en la expresión de la energía de arriba de tal manera que cada término sea un múltiplo del parámetro comóvil ϖ que luego puede ser anulado. Esto sugiere que las ecuaciones resultantes se aplican a cualquier cascarón, y constituyen una descripción del espacio en expansión en términos del factor de expansión R(t) y el parámetro de Hubble H(t). La ecuación de expansión se puede poner en las dos formas equivalentes
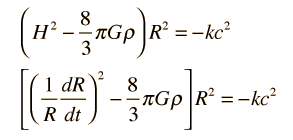
| Expansión Dominada por la Masa |
| Masa y Radiación en el Universo Primitivo |
| Expansión Dominada por la Radiación |
Referencias
Carroll & Ostlie
Cap. 29
| HyperPhysics*****Astrofísica | M Olmo R Nave |