Análisis y Síntesis de Fourier
El matemático Fourier demostró que cualquier función continua, podría ser producida por una suma infinita de ondas seno y coseno. Su resultado tiene implicaciones de largo alcance en la reproducción y la síntesis del sonido. Una onda sinusoidal pura, puede ser convertida en sonido por un altavoz y será percibida como un simple tono continuo puro. Los sonidos de instrumentos orquestales consisten generalmente de una onda fundamental y un complemento de armónicos, que pueden ser considerados como una superposición de ondas sinusoidales, con una frecuencia fundamental f y múltiples enteros de esa frecuencia.
El proceso de descomponer un sonido de un instrumento musical o cualquier otra función periódica, en sus ondas senos y cosenos constituyentes, se llama análisis de Fourier. La onda de sonido se puede caracterizar, en términos de las amplitudes de las ondas sinusoidales componentes que la conforman. Este conjunto de números, indica el contenido de armónicos de un sonido, y a veces es referido como el espectro armónico del sonido. El contenido de armónicos es el más importante determinante de la calidad o timbre de una nota musical sostenida.
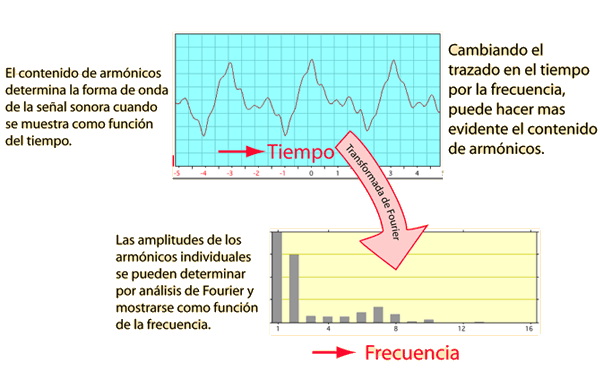
Una vez conocido por el análisis de Fourier el contenido de armónicos de un sonido sostenido musical, se tiene la capacidad de sintetizar ese sonido, mediante una serie de generadores de tonos puros, ajustando correctamente sus amplitudes y fases y juntándolos todos ellos. Esto se denomina síntesis de Fourier.
Una de las ideas importantes para la reproducción del sonido que surge del análisis de Fourier es, que se necesita un sistema de audio de alta calidad para reproducir sonidos de percusión, o sonidos con rápidos transitorios. El sonido sostenido de un trombón, puede ser reproducido dentro de una gama limitada de frecuencias, porque la mayoría de la energía sonora, se encuentra en los primeros pocos armónicos del tono fundamental. Pero si se va a sintetizar el agudo ataque de un platillo, es necesario un amplio rango de altas frecuencias para producir el cambio rápido. Se puede visualizar la tarea de añadir un montón de ondas sinusoidales para producir un pulso agudo, y tal vez se pueda ver que lo que se necesita son grandes amplitudes de ondas con tiempos de subida muy corto (de alta frecuencia) para producir el agudo ataque del platillo. Esta visión del análisis de Fourier se puede generalizar diciendo que, cualquier sonido con un ataque agudo, o un pulso agudo, o los rápidos cambios en la forma de onda como una onda cuadrada, tienen una gran cantidad de contenido de alta frecuencia.
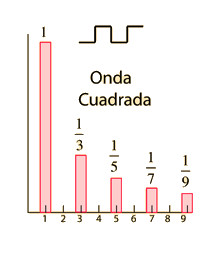 |
Como ejemplo de lo que se aprende de una transformada de Fourier, la transformación de una onda cuadrada muestra que solo tiene armónicos impares y que la amplitud de esos armónicos cae en forma geométrica, con el armónico n-ésimo teniendo 1/n veces la amplitud de la fundamental. |
| Análisis de Fourier y Ondas Geométricas | Series de Fourier |
| Transformada Rápida de Fourier |
Conceptos de Reproducción del Sonido
| HyperPhysics*****Sonido | M Olmo R Nave |