Escalas Musicales
Antecedentes sobre la afinación y el temperamento
supuestos sobre el proceso de la audición humana:
- El oído es sensible a las relaciones de frecuencias (tonos), más que a las diferencias en el establecimiento de los intervalos musicales.
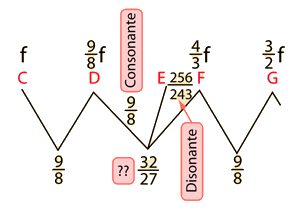
- Los intervalos que se perciben como más consonantes (agradables), se componen de pequeñas proporciones de frecuencias enteras.

|
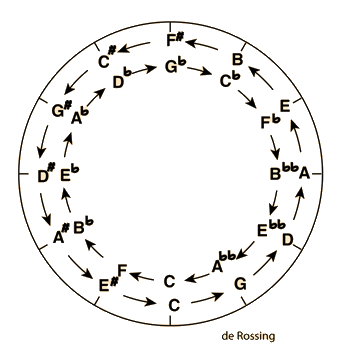
La octava, quinta y cuarta son los intervalos que se han considerado consonantes a lo largo de la historia por prácticamente todas las culturas, de modo que forman una base lógica para la construcción de las escalas musicales. Una estrategia típica del uso universal de estos intervalos consonantes, es el círculo de quintas. |
Temperamento y Escalas Musicales
| HyperPhysics*****Sonido | M Olmo R Nave |