Energía y Espectro del Momento en el Decaimiento Beta
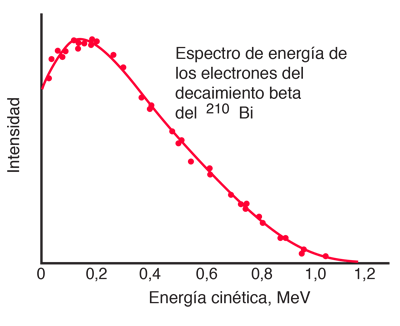 |
La emisión beta tiene un espectro de energía característico. Es acompañado por la emisión de un antineutrino electrónico, que comparte el momento y la energía de la desintegración. Este espectro de energía experimental es de G. J. Neary, Roy. Phys. Soc. (London), A175, 71 (1940). |
A partir de la teoría Fermi del decaimiento beta, la forma de la distribución de energía de esta transición "permitida", está dada aproximadamente por la expresión
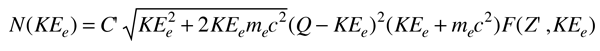
donde F(Z',KEe) se denomina función de Fermi. Es responsable de la interacción nuclear de Coulomb, que desplaza esta distribución hacia energías más bajas, debido a la atracción de Coulomb entre el núcleo hijo y el electrón emitido. (Desplaza hacia arriba la distribución de positrones.) Q representa la producción energética de la transición y, como tal, es el límite superior de la energía cinética del electrón, KEe. La aparente complejidad de la expresión, es en parte debida a que es necesario el uso del momento relativista del electrón.
| La emisión de la antipartícula del electrón, el positrón, también se conoce como decaimiento beta. |  |
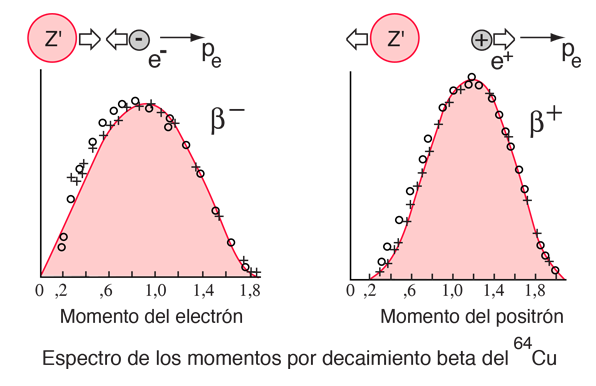
El núcleo del 64Cu, es un buen ejemplo de espectros de momentos, porque decae tanto en emisión de electrones (a 64Zn), como positrones (a 64Ni), con energías de transición comparables. Los espectros experimentales de abajo son de J. R. Reitz, Phys. Rev. 77, 50 (1950). Esto permite ver con claridad, que el espectro del momento del positrón se desplaza hacia un valor mayor, por la repulsión de Coulomb del núcleo.
A partir de la teoría Fermi del decaimiento beta, la forma de la distribución de energía de esta transición "permitida", está dada aproximadamente por la expresión
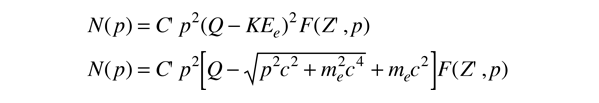
donde F(Z',p) se denomina función de Fermi. Es responsable de la interacción nuclear de Coulomb, y es el origen principal de la diferencia entre las dos curvas de arriba. De nuevo, la expresión parece un poco compleja, debido a que se debe usar la relación relativista entre el momento y la energía del decaimiento beta.
Conceptos de Decaimiento Beta
Referencia
Cohen
Concepts of Nuclear Physics, Sec 11-1
| HyperPhysics*****Nuclear | M Olmo R Nave |