Sistema Holmes-Houtermans para las Isócronas del Plomo

Generalmente se cree que el método más fiable y preciso para determinar la edad de las rocas antiguas incluyendo los meteoritos, es el método de la isócrona del plomo-plomo. Dalrymple llama al método del plomo "el reloj de arena del sistema solar". Se han empleado muchos años de minuciosa investigación, en establecer lo que comúnmente se llama, el sistema de Holmes-Houtermans

Este enfoque de las isócronas Pb-Pb, hace uso de dos de las series naturales radiactivas, la serie del uranio-238 y la serie del uranio-235, que se relacionan entre sí, por el hecho de que la razón isotópica ²³⁸U = 137,88 ²³⁵U, se ha encontrado que es consistente con las rocas de la Tierra, la Luna y los meteoritos. Las dos series terminan en diferentes isótopos de plomo finales:

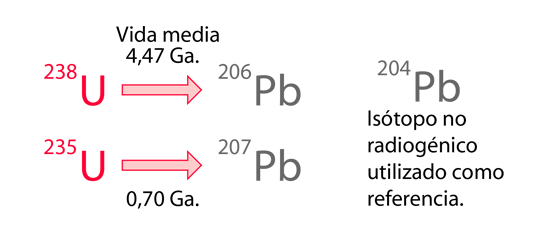
y hay un tercer isótopo de plomo, el ²⁰⁴Pb, que no se forma en ningún proceso radiactivo, y por lo tanto, puede ser utilizado como una referencia. Por ello, las ecuaciones relacionadas con el decaimiento, permiten el trazado de la dependencia de la relación ²⁰⁷Pb/²⁰⁴Pb, sobre la relación ²⁰⁶Pb/²⁰⁴Pb, una fórmula que cambia con el tiempo para producir una "curva de crecimiento" como la que se ilustra arriba. Se forman diferentes curvas de crecimiento, con diferentes cantidades de ²³⁸U en el mineral en el momento de la cristalización. Pero los puntos sobre las diferentes curvas de crecimiento de los minerales constituyentes de la roca sin perturbar, se encuentran a lo largo de una línea recta, la "isócrona". La pendiente de esta isócrona es una medida del tiempo T, desde el estado fundido hasta la cristalización o la formación de la roca. En un estado fundido, los diferentes isótopos habrían formado una mezcla en equilibrio, ya que son químicamente idénticos.

El desarrollo del enfoque de Holmes-Houtermans sigue los fundamentos de la desintegración radiactiva, que actúa como un reloj. A pesar de que la desintegración de ²³⁸U a ²⁰⁶Pb pasa por cerca de 14 pasos, todo el proceso llega a ese punto final y puede ser razonablemente caracterizado por una semi vida efectiva de 4,47 Gy.

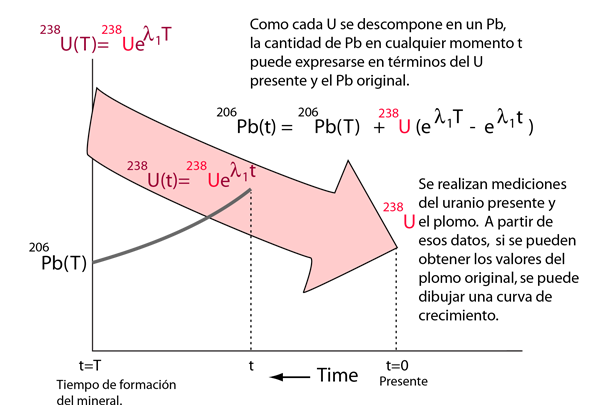
Dado que se miden los valores actuales de uranio y plomo, se acostumbra a dejar correr el reloj hacia atrás, y modelar el proceso como un aumento exponencial de uranio. Puesto que el ²⁰⁴Pb, se usa como un estándar, todas las cantidades se expresan como proporciones respecto del contenido de ²⁰⁴Pb. Se puede desarrollar una curva de crecimiento del ²⁰⁶Pb, basada en el contenido experimental del ²³⁸U.

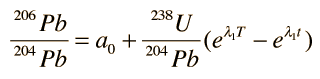
Para el ²³⁵U, el proceso es el mismo, dando lugar a la curva de crecimiento del ²⁰⁷Pb

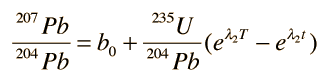
En estas curvas de crecimiento de las proporciones isotópicas de plomo respecto del tiempo, a₀ y b₀ son las relaciones isotópicas del plomo en el momento de la formación T:

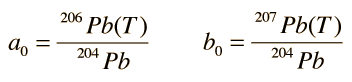
y λ₁ y λ₂ son las constantes de decaimiento de ²³⁸U y ²³⁵U respectivamente.

Aunque puede ser útil una curva de crecimiento en función del tiempo, es mas ventajoso trazar curvas de crecimientos en términos de proporciones isotópicas ²⁰⁷Pb/²⁰⁴Pb versus ²⁰⁶Pb/²⁰⁴Pb. Esto se hace posible, por el hecho de que la razón isotópica de los isótopos de uranio es consistente en las rocas de la Tierra, la Luna y los meteoritos, y se puede utilizar para acoplar las curvas de crecimiento de arriba. Usando esta relación

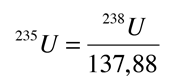
La curva de crecimiento del ²⁰⁷Pb de arriba, se puede escribir

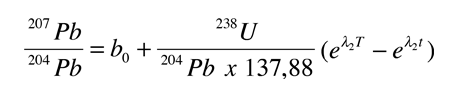
Esto acopla las ecuaciones de crecimiento de tiempo, y permite el trazado de una curva de crecimiento, en términos de las proporciones de isótopos de plomo en lugar de tiempo, como se muestra en la ilustración superior. Se obtienen diferentes curvas de crecimiento, para diferentes contenidos de uranio. El contenido de uranio se denota por el símbolo µ y las curvas de crecimiento en la ilustración de arriba, muestra que las curvas con mayores valores de µ, dan en ese tipo de trazado, curvas más altas.

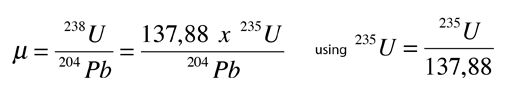
Si se tiene una determinada muestra de roca con varios minerales diferentes dentro de ella, no habrá en general una variedad de valores de µ y por lo tanto varias curvas de crecimiento diferentes. El paso conceptual final en el sistema Holmes-Houtermans, es entonces señalar que una proporción de ecuaciones de crecimiento para los dos isótopos de plomo radiogénicos, da una relación que es independiente del contenido de uranio µ, da la ecuación de una línea recta, una isócrona.

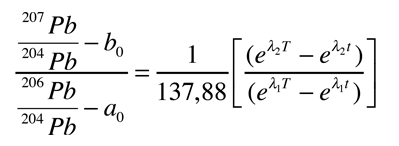
Refiriéndose de nuevo a la ilustración de arriba, si se sitúa en un valor de tiempo t, se produce una línea recta que cruzará las curvas de crecimiento de los diferentes valores de µ. Si en esa ilustración se situa en t = 0, que representa el momento actual, se obtiene la isócrona actual. La pendiente de la isócrona actual, da el valor T de la formación de la roca desde su estado fundido. La ecuación para la edad T es trascendental y no puede resolverse directamente, pero se puede resolver gráficamente o por aproximaciones sucesivas.

El gran desafío restante en el uso de las isócronas Pb-Pb para determinar la edad de las rocas, fue la determinación de las relaciones primigenias de los isótopos de plomo, a₀ y b₀, ya que son necesarios para determinar la pendiente de la isócrona actual. La experimentación durante un número de años, ha establecido el vínculo entre las rocas más antiguas de la Tierra y los meteoritos, y parece que estos forman las mejores referencias para determinar a₀ y b₀. En particular, el mineral troilita del meteorito del Cañón del Diablo, ha mostrado el más bajo contenido de uranio original, y se usa generalmente como el estándar para determinar las concentraciones originales.

Los valores de a₀ y b₀ son de Tatsumoto, Knight and Allegre, 1973. Los otros valores son los primeros de Patterson. Dalrymple describe el resultado de Tatsumoto, et al, como el "valor generalmente aceptado de plomo primigenio en el sistema solar."