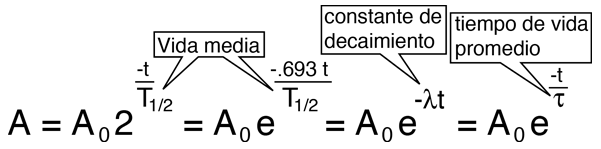
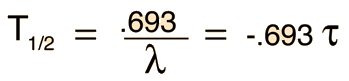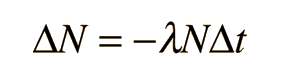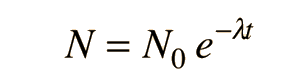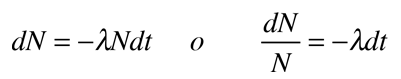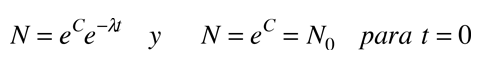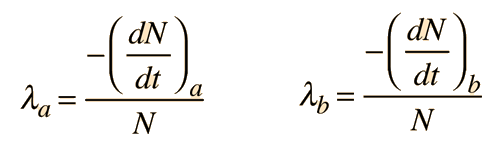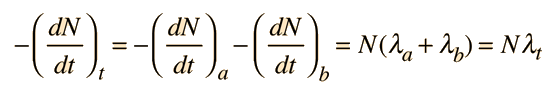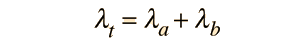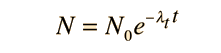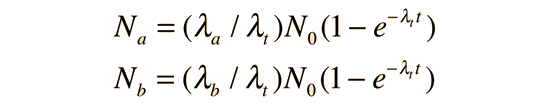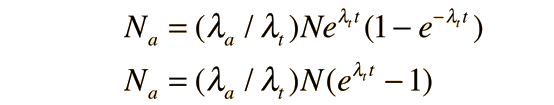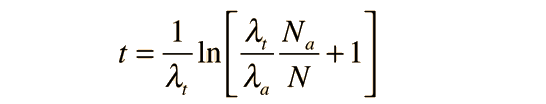Radioactive Decay by Multiple Pathways
Often a radioactive nucleus will decay by two or more pathways, yielding different final products. If there are two modes, leading to products a and b, then we can represent the decay rates by these two modes by partial decay constants λa and λb defined by
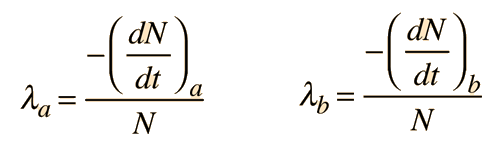
Where N is the number of the parent radioactive nuclei. The total decay rate dN/dt is then given by
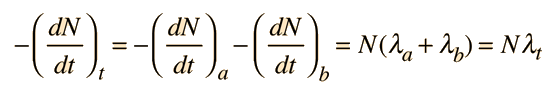
The decay is governed by the total decay rate since both are proceeding simultaneously.
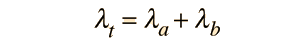
The number of parent nuclei remaining at time t is then
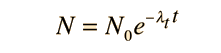
and the amounts of the decay products a and b are
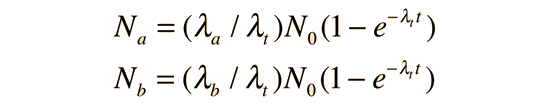
Note that the individual decay constants λa and λb never appear in the exponential. Both processes continue to proceed and the rate of decay is determined by the sum of their decay constants. This process can be extended to more pathways if all proceed from the same parent nucleus.
If you sought to use the measured population of the isotopes to date a sample, you would not have access to the value N0 of the parent isotope, and would need to recast the above expressions in terms of the current measured value N of the parent. Using product a, the expression for the population Na then becomes
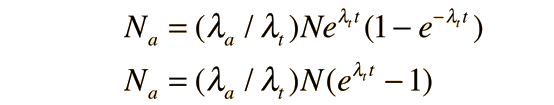
and this can be solved algebraically for the time t:
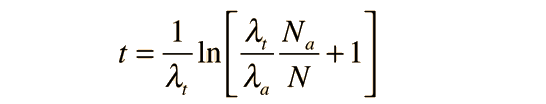
This is the approach taken in potassium-argon dating where there are decay modes to both argon and calcium.
|