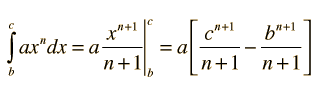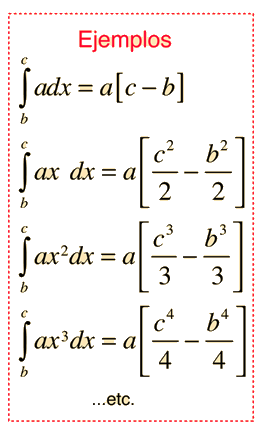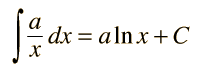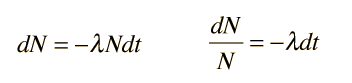Integrales de Polinomios
|
La integral de cualquier polinomio es la suma de las integrales de sus términos. El término general de un polinomio se puede escribir 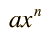 y la integral indefinida de ese término es 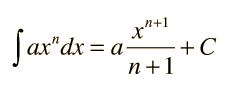 donde a y C son constantes. La expresión se aplica tanto a valores positivos como negativos de n excepto en el caso especial de n=-1. En los ejemplos, C se establece igual a cero. Si en la integración se establecen límites definidos, se llama entonces una integral definida. |
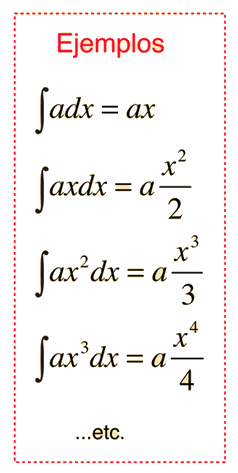
|
Caso para n = -1
Aplicaciones
| HyperPhysics*****HyperMath*****Cálculo | M Olmo R Nave |