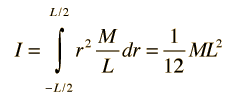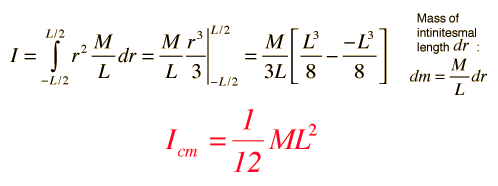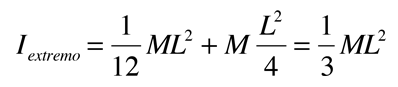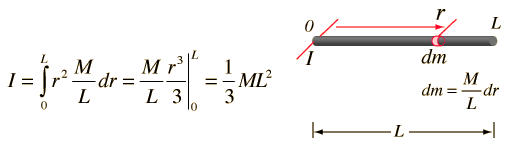Rotacional y Lineal. Ejemplos
Se coloca una masa m, en una barra de longitud r y masa despreciable, y se le obliga a girar alrededor de un eje fijo. Si la masa se la libera de una orientación horizontal, podemos describir su movimiento en términos de fuerza y aceleración con la segunda ley de Newton para movimiento lineal, o como una rotación pura sobre el eje con la segunda ley de Newton para la rotación. Esto proporciona un marco para la comparación sobre un mismo sistema, de las cantidades lineales y de rotación. Este proceso nos lleva a la expresión del momento de inercia de una masa puntual.
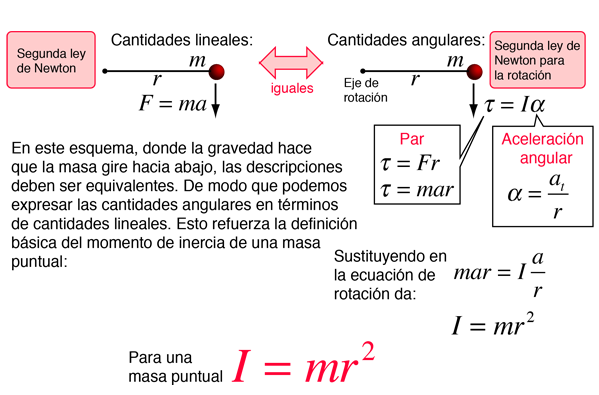
Conceptos sobre Momento de Inercia
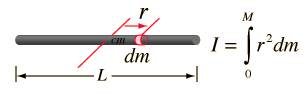
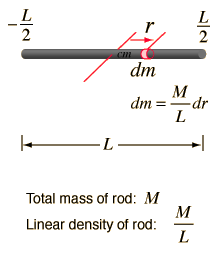
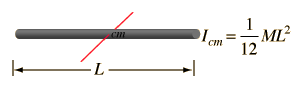
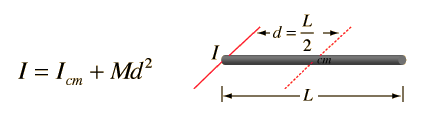
Momento de Inercia. Ejemplos
| HyperPhysics*****Mecánica*****Rotación | M Olmo R Nave |