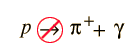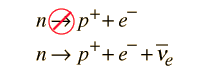Cruzamiento Simétrico
Si se observa que se produce una interacción de partículas
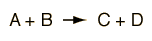
, entonces, se puede anticipar interacciones relacionadas por el hecho de que cualquiera de las partículas puede ser reemplazada por su antipartícula en el otro lado de la interacción. Esto se conoce comúnmente como "simetría de cruce." La observación de la interacción de arriba implica la existencia de las siguientes interacciones.
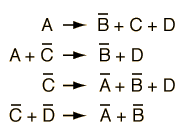
La barra superior indica la antipartícula. La simetría de cruce se aplica a todas las partículas conocidas, incluyendo el fotón que es su propia antipartícula. Un ejemplo del principio de cruzamiento es el de la relación entre la dispersión de Compton y la aniquilación electrón-positrón..
| Mostrar en Diagramas de Feynman |
Mediante el examen, se puede observar que estas dos interacciones están relacionadas por la simetría de cruce. Se podría decir entonces que la observación de la dispersión de Compton implica la existencia de la aniquilación de par, y predice que va a producir un par de fotones.
Otro ejemplo de cruce simétrico puede haber conducido a Reines y Cowan a su experimento para la detección del neutrino. Si de la reacción del decaimiento del neutrón, se toma el electrón producido al otro lado y se convierte en un positrón, entonces se tiene la reacción que utilizaron.
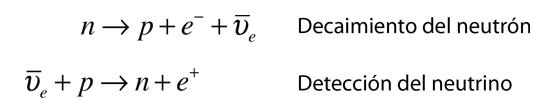
Conceptos de Partícula
Leyes de Conservación de Partículas
Referencias
Griffiths
Cap. 2
| HyperPhysics*****Física Cuántica | M Olmo R Nave |