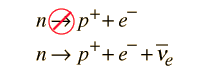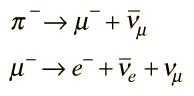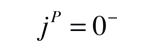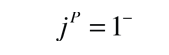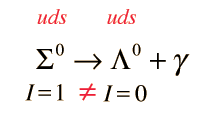Interacciones de Partículas y Leyes de Conservación

En el desarrollo del modelo estándar de partículas, se observa que ciertos tipos de interacciones y decaimientos son comunes, mientras otros parecen estar prohibidos. El estudio de las interacciones ha dado lugar a una serie de leyes de conservación que las rigen. Estas leyes de conservación son una ampliación de las leyes clásicas de conservación, tales como la conservación de la energía, la carga, etc, que aún se aplican en el ámbito de las interacciones entre partículas. Las firmes leyes generales de conservación son, la conservación del número bariónico, y la conservación del número de leptones. A las diferentes partículas fundamentales se le han asignado específicos números cuánticos, y hay otras leyes de conservación que están asociadas con estos números cuánticos.

Desde otro punto de vista, parecería que cualquier partícula localizada de masa finita, debería ser inestable, ya que la descomposición en varias partículas más pequeñas, proporciona muchas más formas de distribución de la energía, y por lo tanto tendría una mayor entropía. Esta idea se llegó a señalar como un principio llamado "principio totalitario", que podría formularse como "todo proceso que no esté prohibido, debe ocurrir". Desde este punto de vista, cualquier proceso de decaimiento que se espere pero no se observe, debe ser impedida su producción por alguna ley de conservación. Este enfoque ha sido fructífero en la ayuda para determinar las reglas del decaimiento de partículas.

Las leyes de conservación de la paridad, el isospín, y la extrañeza, han sido desarrolladas mediante la observación detallada de las interacciones de partículas. La combinación de la conjugación de carga (C), la paridad (P) y la inversión del tiempo (T), se considera que es una operación fundamental de simetría -todas las partículas físicas e interacciones, parecen ser invariantes bajo esta combinación-. Esta simetría llamada invariancia CPT, se sumerge en las profundidades de nuestra comprensión de la naturaleza.

Otra parte del conjunto de herramientas de la física de alta energía en anticipar lo que se puede esperar de las interacciones, es la "simetría de cruce". Cualquier interacción que se observe, se puede utilizar para predecir otras interacciones relacionadas, mediante el "cruce" de cualquier partícula a través del símbolo de la reacción, y convirtiéndola en su antipartícula.

Conservación del Número de Bariones

La naturaleza tiene normas específicas para las interacciones de partículas y los decaimientos. Estas reglas se han resumido en términos de leyes de conservación. Una de las más importantes es la conservación del número bariónico. A cada uno de los bariones se le asigna un número bariónico B=1. Esto puede ser considerado como equivalente a asignar a cada quark un número bariónico de 1/3. Esto implica que los mesones, con un quark y un antiquark, tienen un número bariónico B=0. Ningún proceso de decaimiento o interacción conocida en la naturaleza, cambia el número neto de bariones.

El neutrón y todos los bariones más pesados, decaen directamente en protones o eventualmente forman protones. El protón es el barión menos masivo. Esto implica que el protón no tiene a dónde ir, sin violar la conservación del número bariónico, así que si se mantiene la conservación de este número exactamente, el protón es completamente estable contra los decaimientos. Una predicción de la gran unificación de fuerzas, es que el protón debería tener la posibilidad de decaimiento, de modo que esa posibilidad está siendo investigada experimentalmente.

La conservación del número de bariones prohíbe un decaimiento del tipo

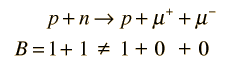
pero con la suficiente energía, se permite la producción del par en la reacción

El hecho de que se observe el decaimiento

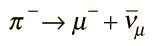
implica que no hay un correspondiente principio de conservación del número de mesones. El pión es un mesón compuesto por un quark y un antiquark, y en el lado derecho de la ecuación solamente hay leptones. (De manera equivalente, al mesón se le puede asignar un número bariónico 0.)

Conservación del Número de Leptones

La naturaleza tiene normas específicas para las interacciones de partículas y los decaimientos. Estas reglas se han resumido en términos de leyes de conservación. Una de las más importantes es la conservación del número de leptones. Esta regla es un poco más complicada que la conservación del número bariónico, porque hay un requisito separado para cada uno de los tres conjuntos de leptones, el electrón, el muón y el tau, y sus neutrinos asociados.

El primer ejemplo significativo se encontró en el decaimiento del neutrón. Cuando se observó el decaimiento del neutrón en un protón y un electrón, no encajaba en el modelo de decaimiento de dos partículas. Es decir, el electrón emitido no tiene una energía definida como es requerido por la conservación de la energía y el momento para un decaimiento de dos cuerpos. Esto implicó la emisión de una tercera partícula, que ahora identificamos como el antineutrino electrónico.

La asignación de un número leptónico de 1 al electrón y -1 para el antineutrino electrónico, mantiene el número leptónico igual a cero en ambos lados de la segunda reacción de arriba, mientras que la primera reacción no conserva el número leptónico.

La observación de los siguientes dos procesos de desintegración, lleva a la conclusión de que hay un número leptónico separado para los muones que también debe ser conservado.

La primera reacción anterior (decaimiento del pión) se sabe que es un decaimiento de dos cuerpos por el hecho de que se observa la bien definida energía del decaimiento del muon. Sin embargo, la desintegración del muón en un electrón produce una distribución de energías de electrones, que muestra que al menos es un decaimiento de tres cuerpos. Para que se conserven ambos, número leptónico del electrón y número leptónico del muón, las otras partículas deben ser un antineutrino electrónico y un neutrino muón.

Paridad

Una de las leyes de conservación que se aplica a las partículas está asociada con la paridad.

Los quarks tienen una paridad intrínseca que se define como +1 y para un antiquark una paridad =-1. Los nucleones se definen que tienen paridad intrínseca +1. Para un mesón con quark y antiquark con espines antiparalelos (s=0), entonces la paridad está dada por

La paridad del mesón viene dada por

Los estados de energía más bajos de los pares quark-antiquark (mesones), tienen espín cero y paridad negativa. Se llaman mesones pseudoescalares. Los nueve mesones pseudoescalares se puede mostrar en los diagramas del mesón. Un tipo de notación de estos estados, indica su momento angular y la paridad

Se producen estados excitados de mesones en los que los espines de los quarks están alineados, los cuales con momento angular orbital cero, da j=1. Tales estados se llaman mesones vectoriales.

Los mesones vectoriales tienen el mismo espín y paridad que los fotones.

Todos los neutrinos resultan ser "zurdos", con una paridad intrínseca de -1, mientras que los antineutrinos son diestros, paridad =+1.

Isospín

El isospín es un término introducido para describir grupos de partículas que tienen casi la misma masa, tales como el protón y el neutrón. Este doblete de partículas se dice que tienen isoespin 1/2, con proyección +1/2 el protón, y -1/2 el neutrón. Los tres piones componen un triplete, lo que sugiere isoespin 1. Las proyecciones son +1 para el positivo, y 0 y -1 para los piones neutros y negativos respectivamente. El isospín se usa como eje en los diagramas de partículas, siendo el otro eje la extrañeza. El isospín no está realmente girando, y no tiene las unidades del momento angular -se ha insertado el término espín, porque la adición de los isoespines sigue las mismas reglas que los espines-.

El isospín es una cantidad adimensional asociada con el hecho de que la interacción fuerte es independiente de la carga eléctrica. Cualquiera de los dos miembros del doblete isospin protón-neutrón, experimenta la misma interacción fuerte: protón-protón, protón-neutrón, neutrón-neutrón, Es decir, tienen la misma fuerza de atracción fuerte.

A nivel de quark, los quarks up y down forman un doblete isospín (I=1/2) y se asigna la proyección I₃ = +1/2 al quark up, y I₃ =-1/2 al quark down. (Aquí se usa el subíndicet 3 para el tercer componente, en lugar de la z usada con el espín y el momento angular orbital, porque la mayoría de la literatura en los textos así lo hace). A los otros quarks se le asigna el isospín I=0. El isospín se relaciona con los otros números cuánticos de las partículas por

Esta relación se denomina la fórmula de Gell Mann-Nishijima. Algunas referencias utilizan T para el isospín, pero parece que la mayoría usa I para el isospín y T para el isospín débil.

El isospín se asocia con la ley de conservación que requiere decaimientos de interacción fuerte para su conservación, como se ilustra por el proceso

que no implica ninguna transmutación de quarks, por lo que sería de esperar decaimiento por interacción fuerte. Sin embargo, no se conserva el isospín, y se observa decaimiento por interacción electromagnética, pero no por interacción fuerte. La discriminación experimental se efectuó por la observación del tiempo de vida del decaimiento, suponiendo por el principio totalitario que si se pudiera descomponerse por la interacción fuerte, lo sería