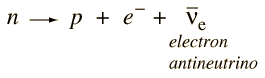Los Neutrinos Zurdos

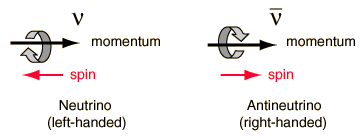
Las orientaciones relativas de los momentos de espín y lineal de los neutrinos y antineutrinos, es aparentemente fija e intrínseca de las partículas.

Esta propiedad está relacionada con el concepto de paridad y con las leyes de conservación que aplica a las interacciones entre partículas.

En los neutrinos, el espín es siempre opuesto al momento lineal y esto se conoce como ser "zurdo", mientras que los antineutrinos son siempre "diestros". Esto evoca la imagen de la regla de la mano derecha del momento angular vectorial. En esta convención, los dedos de la mano derecha se utilizan para indicar el sentido de giro o movimiento orbital, con el pulgar apuntando en la dirección definida del momento angular. El momento de la partícula se utiliza para definir una dirección preferida en el espacio, y si se curvan los dedos de la mano derecha para mostrar el sentido del "espín" del antineutrino, el pulgar apuntaría en la dirección de este momento. Por lo tanto es una partícula "diestra". En el neutrino, se tendría que usar los dedos de la mano izquierda para conseguir que el pulgar apunte en la dirección del momento lineal.

Antes de 1956, toda la evidencia experimental disponible sugería que "zurdo" versus "diestro" no era una caracterización significativa de las interacciones de partículas, ya que las leyes de la física parecían conservar la paridad. El experimento demostró que las interacciones que proceden de las fuerzas fuertes y electromagnéticas "conservan la paridad". Pero el trabajo teórico de Lee y Yang y el experimento con la desintegración del cobalto-60 de Wu mostró que esta desintegración por la interacción débil no conservaba la paridad. Esto hace que las interacciones débiles que emiten neutrinos o antineutrinos violen la conservación de la paridad.

La propiedad que aquí ha sido llamado para zurdos y diestros, a veces se llama "helicidad". La helicidad de una partícula se define como la relación m_s/s, o la componente z del espín, dividido por la magnitud del espín. Según esta definición, en este caso, la helicidad es +1 para un antineutrino diestro, y -1 para un neutrino zurdo.

Sección Eficaz de los Neutrinos

La sección eficaz nominal del neutrino en la interacción con el nucleón aumenta con la energía, tal como se indica en los datos de la derecha citadas por Rohlf. Los datos que se muestran a la derecha, se tomaron a energías muy por encima de la gama de la desintegración radiactiva de los neutrinos. Cuando se extrapola la pendiente de la línea recta de la derecha, a 1 MeV, da una sección eficaz de unos 10-45 m2. Esto todavía es tres órdenes de magnitud mayor que la sección eficaz medida por Cowan y Reines en su experimento pionero. El comentario de Rohlf sobre esta dependencia lineal de la energía de la sección eficaz, era debido a las grandes energías del neutrino en comparación con las energías de masa de los quarks, por lo que la extrapolación a las energías de desintegración radiactiva normal, era pedir demasiado.

La detección original de los neutrinos por Reines y Cowan se basaba en la reacción

Esta interacción está relacionada con el decaimiento del neutrón, por la simetría de cruce, el ejemplo mas simple del decaimiento beta. De hecho, es a veces referido como el "decaimiento beta inverso". Así parece que el estudio del decaimiento beta, podría dar una aproximación de la sección eficaz de la interacción de neutrinos.

El enfoque para calcular la sección eficaz de la interacción, se basa en la Regla de Oro de Fermi, y si se puede encontrar un elemento matriz de la interacción débil en una de estas reacciones, debería ser comparable en la otra.

Las estimaciones de la fuerza de acoplamiento de la interacción débil, provienen de la aplicación de la teoría de Fermi del decaimiento beta, a algunos casos especiales. Krane hace esto, para llegar a una estimación de 10^-43 cm² = 10^-47 m² para la sección eficaz del neutrino en el rango de energías de la desintegración beta. Esto es alrededor de 20 órdenes de magnitud menor, que la sección eficaz de dispersión de ¡dos nucleones a baja energía!.

Con esta sección eficaz nominal, se pueden hacer algunas estimaciones de las tasas de interacción. Multiplicando la sección eficaz por la densidad de nucleones, da un número de interacciones por metro, y la inversa de eso, es una estimación de la trayectoria libre media. En el agua, con una densidad de 1000 kg/m³, puede estimarse el recorrido libre medio de un neutrino a partir

Se puede tener una perspectiva sobre estas distancias, comparándola con un año luz

Así que esta estimación de la trayectoria libre media es de ¡más de un año luz en plomo! Una declaración cualitativa bastante común en los textos de física, es que el camino libre medio de un neutrino es de aproximadamente un año luz de plomo. Griffiths hace esta declaración: "un neutrino de energía moderada, podría fácilmente ¡penetrar mil años luz de plomo!." Esta sección eficaz, también puede ser utilizada para estimar el número de eventos que se pueden esperar, en un detector de determinado tamaño.

El cálculo de Bahcall sobre el flujo de neutrinos solares es de aproximadamente 5 x 10⁶ /cm²s en la superficie de la Tierra. En lo que se llama el " "problema de los neutrinos solares", en los primeros experimentos solamente se midieron alrededor de un tercio a un medio de ellos. Los experimentos recientes en el Observatorio de Neutrinos de Sudbury sugieren que la oscilación de los neutrinos, transmutan algunos de los neutrinos electrónicos solares, en muón y neutrinos tau. Cuando se tiene en cuenta esto en los últimos experimentos del SNO, el flujo resulta muy de acuerdo con la estimación de Bahcall.