Probabilidades de Transición y Regla de Oro de Fermi

Uno de los fallos prominentes del modelo de Bohr para los espectros atómicos era, que no se podía predecir que una línea espectral fuera más brillante que otra. Desde la teoría cuántica vino una explicación en términos de funciones de onda, y para situaciones en las que la probabilidad de transición es constante con el tiempo, por lo general se expresa en una relación llamada regla de oro de Fermi.

En términos conceptuales generales, la tasa de transición depende de la fuerza de acoplamiento entre el estado inicial y final de un sistema, y del número de formas en que la transición puede ocurrir (es decir, la densidad de estados finales). En muchas situaciones físicas la probabilidad de transición es de la forma

La probabilidad de transición λ se denomina también la probabilidad de descomposición, y se relaciona con el tiempo de vida media τ del estado, por λ = 1/τ. La forma general de la regla de oro de Fermi puede aplicarse a las transiciones atómicas, decaimiento nuclear, dispersión ... una gran variedad de transiciones físicas.

Una transición procederá más rápidamente si el acoplamiento entre los estados inicial y final es más fuerte. Este término de acoplamiento se llama tradicionalmente, el "elemento matriz" de la transición: este término proviene de una formulación alternativa de la mecánica cuántica en términos de matrices, en lugar de las ecuaciones diferenciales del enfoque de Schrodinger. El elemento matriz puede ser colocado en forma de una integral, donde la interacción que provoca la transición, se expresa como un potencial V, que opera sobre la función de onda del estado inicial. La probabilidad de transición es proporcional, al cuadrado de la integral de esta interacción sobre todo el espacio adecuado al problema.

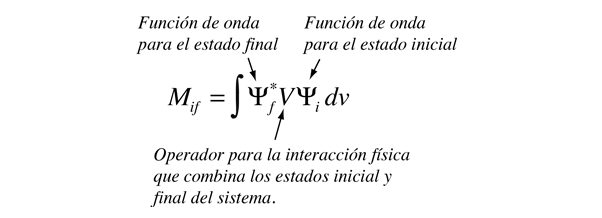
Este tipo de enfoque de integral utilizando las funciones de onda, es de la misma forma general que el usado para encontrar el "valor esperado" o valor promedio esperado, de cualquier variable física en la mecánica cuántica. Pero en el caso del valor esperado de una propiedad como la energía del sistema, la integral tiene la función de onda que representa el estado propio del sistema, en ambos lugares de la integral.

La probabilidad de transición es también proporcional a la densidad de estados finales r_f. Es bastante común que el estado final esté compuesto de varios estados con la misma energía, -tales estados se dice que son estados "degenerados"-. Esta degeneración se expresa a veces como un "peso estadístico", que aparece como un factor en la probabilidad de transición. En muchos casos habrá un continuo de estados finales, por lo que esta densidad de estados finales, se expresa como una función de la energía.